Question

При каких значениях a уравнение x²-(2a+2)x-2a-3=0 имеет два различных отрицательные корни?

Answer 1

D=(a+1)^2+2a+3=a^2+4a+4>0

(a+2)^2>0

a>-2 U a<-2

-2a-3>0

a<-3/2

-2<a<-3/2

2a+2<0

a<-1

ответ -2<a<-3/2

Answer 2

x²-(2a+2)x-2a-3=0;

За теоремой Виета:

$\left \{ {{x_{1}+x_{2}=-b,} \atop {x_{1}*x_{2}=c;}} \right.$

$\left \{ {{x_{1}+x_{2}=2a+2,} \atop {x_{1}*x_{2}=-2a-3;}} \right.$

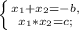
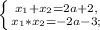
То есть, чтобы уравнение имело два различных отрицательные корни:

$\left \{ {{x_{1}+x_{2}<0,} \atop {x_{1}*x_{2}0;}} \right.$

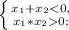
или:

$\left \{ {{b0,} \atop {c0;}} \right.$

$\left \{ {{-2a-20,} \atop {-2a-30;}} \right.$

$\left \{ {{-2a2,} \atop {-2a3;}} \right.$

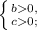
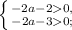
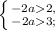
Меняем знак, так как делим неравенства на отрицательные числа (на -2)

$\left \{ {{a<-1,} \atop {a<-3/2;}} \right.$

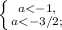
Общее: a<-3/2.

ответ: при a< -1,5.