а) модуль числа а это само число а, если оно взято со знаком + и число !а!=-а, если а число отрицательное, т.е. взято со знаком -. Отсюда можно сделать вывод что модуль никогда не может быть равен отрицательному числу, абсолятное значение всегда положительно, поэтому единственное число, удоволтворяющее !x!=-x это 0, поэтому под буквой а можешь отметить только 0
б) Во втором случае этому уравнению будет эквивалентна система уравнений вида
x+2=x+2 - тождественно верно
x+2=-(x+2)-решаем
x+2=-x-2
x+x+2+2=0
2x+4=0
2x=-4
x=-2
Значит все точки числовой прямой начиная с x=-2 и в положительнную сторону будут удоволетворять уравнению, отсюда ответ будет вся числовая прямая начиная с -2 и больше
1.
а) 15·(-7) = -(15·7) = -105
б) -14·(-17) = 14·17 = 238
в) -0,9·4,1 = -(0,9·4,1) = -3,69
г)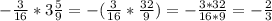 
2.
а) -84:14 = -(84:14) = -6
б) -42:(-6) = 42:6 = 7
в) 0,114:(-0,76) = -(0,114:0,76) = -0,15
г)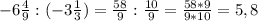 
3.
а) -1,6b = -6,48
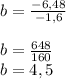
б) а:2,4 = -4,8
а = -4,8*2,4
а = -11,52
4.
Представьте числа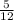 
и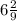 
в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых.
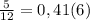
0,41(6)≈0,42
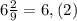
6,(2)≈6,222.
5.
|х|<86
-86<x<86
Целые неотрицательные решения неравенства: от 0 до 85. Общее количество 86.
Целые отрицательные решения неравенства: от -1 до -85. Общее количество 85.
Всего целых решений неравенства: 86+85 = 171.
Круг - это 360 градусов. Спицы делят его на 25 равных частей.
Угол, образованный двумя соседними спицами - это как раз одна из 25 таких частей, и равен он 360/25=14,4 градуса.