№1
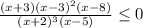
находим корни числителя и знаменателя:
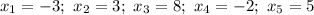
(x-3)^2 - всегда принимает неотрицательные значения. Значит при переходе через точку 3 неравенство знак не поменяет.
Используем метод интервалов:
точки (-2) и 5 - выколотые.
+ - + + - +
-------[-3]--------(-2)-------[3]--------(5)--------[8]---------->x
![x\in [-3;-2)\cup (5;8] \cup \{ 3 \}](/tpl/images/0999/4162/b28f6.png)
ответ:
№2
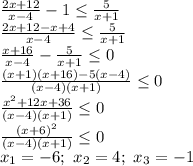
точки (-1) и 4 - выколотые
+ + - +
------[-6]------(-1)------(4)------->x
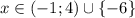
ответ: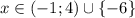
№3
замена:
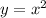
получим:
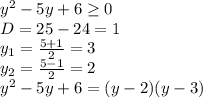
обратная замена:
+ - + - +
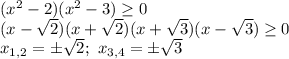
-------[-√3]-------[-√2]--------[√2]-------[√3]-------->x
![x\in (-\infty;-\sqrt{3}]\cup [-\sqrt{2};\sqrt{2}]\cup [\sqrt{3};+\infty)](/tpl/images/0999/4162/cc812.png)
ответ:
B) = -2ху(6х^2+2.8у)