Разложим уравнение на множители.
0,5 * х * (3 * х2 / (0,5 * х) - 0,5 * х / (0,5 * х) = 0.
0,5 * х * (6 * х - 1) = 0.
Данное равенство будет выполняться, когда:
0,5 * х = 0 и 6 * х - 1 = 0.
х1 = 0 / 0,5 = 0.
6 * х2 = 0 + 1.
6 * х2 = 1.
х2 = 1/6.
Выполним проверку для х1 = 0:
3 * 02 - 0,5 * 0 = 0.
0 - 0 = 0.
0 = 0.
х1 = 0 является решением данного уравнения.
Выполним проверку для х2 = 1/6:
3 * (1/6)2 - 0,5 * 1/6 = 0.
3 * 1/36 - 5/10 * 1/6 = 0.
1/12 - 5/60 = 0.
1/12 - 1/2 = 0.
0 = 0.
х2 = 1/6 тоже является решением данного уравнения.
ответ: корни уравнения х1 = 0 и х2 = 1/6.
Объяснение:Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева. Равносильные уравнения — это те, в которых совпадают множества решений.
Объяснение:
1) представьте систему в матричной форме
2) умножьте строку 1на (-2) и прибавить результат к строке 2
Умножьте строку 1на (-1) и прибавить результат к строке 3:
3) умножьте вторую строку на -1
4) умножить строку 3 на 2 и прибавить результат к строке 1.
Умножьте строку 3 на 5 и прибавьте результат к строке 2
5) разделить строку 2 на 14
6) умножить строку 2 на -7 и прибавить результат к строке 1.
Умножить строку 2 на -2 и прибавить результат к строке 3
7) умножить строку 3 на -1
8) преобразовать расширенную матрицу систему линейных уравнений
ответ: решение систем уравнений является упорядоченная тройка (х,у,z)
Решение на фотке

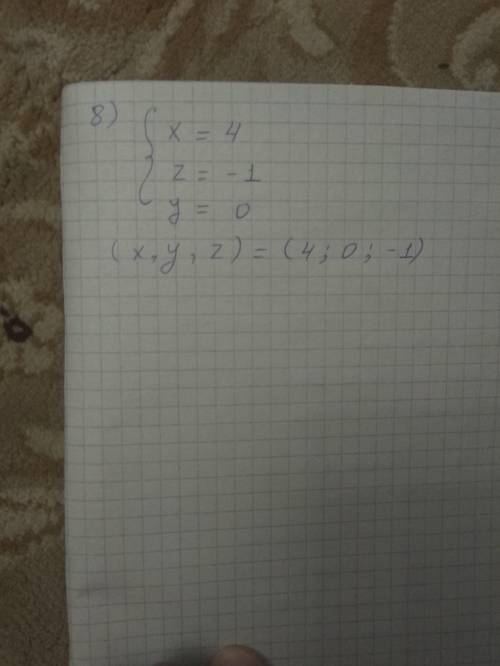
tg a > 0;
cos^2 a = 1 - sin^2 a = 1 - ( -15/17)^2 = 1 - 225/289 = 64/289;
cos a = - 8/17;
tg (3pi/2 - a) = tg a = sin a / cos a = ( - 15/17) / ( - 8/17) = 15/8;