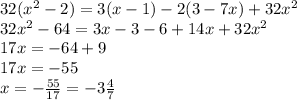
ответ: h(t) = 9t - 2t², h - высота в м, t - время в секундах.
а) На какой высоте будет мяч через 2 секунды
t=2
h(2)=9*2-2*2²=10 метров
б) Через сколько секунд мяч будет находиться на высоте 10 м?
h=10
9t--2t²=10
2t²-9t+10=0
D=9²-4*2*10=1
t₁=(9-1)/4=2 с
t₂=(9+1)/4=2.5 с
Значит на высоте 10 м мяч буде находится через 2 с и через 2,5 с
в) Какой наибольшей высоты достиг мяч?
h(t) = 9t - 2t² парабола, ветви направлены вниз, значит точка максимума в вершине параболы:
t₀=-9/(-2*2)=2.25 c
h(2.25)=9*2.25-2*2.25²=20.25-10.125=10.125 м максимальная высота
Объяснение:надеюсь поймёшь
Объяснение:
|x -1| + |x +3| ≤ 4
Решим это неравенство методом интервалов.
Найдем нули подмодульных выражений:
х - 1 =0 → х = 1
х + 3 = 0 → х = - 3
Эти значения разбивают числовую ось на три интервала:
х ∈ (-∞; - 3] ; (-3; 1]; (1; + ∞)
Решим заданное неравенство на каждом из этих промежутков.
1) 1) x∈ (-∞; - 3], при этом неравенство примет вид:
- (х - 1) - (х + 3) ≤ 4
-х + 1 - х - 3 ≤ 4
-2х ≤ 6
х ≥ - 3
Пересекая найденное решение x∈ [- 3; +∞) c рассматриваемым интервалом x∈ (-∞; - 3] , получаем решение x = - 3
2) х ∈ (-3; 1]
- (х - 1) + х + 3 ≤ 4
0*х ≤ 4 → х - любое число. Учитывая интервал, х х ∈ (-3; 1]
3) х ∈ (1; + ∞)
х - 1 + х + 3 ≤ 4
2х ≤ 2
х ≤ 1 → х ∈ (- ∞; 1]
Для получения окончательного ответа объединим полученные решения:
x ∈ [- 3] ∪ (-3; 1] ∪ (- ∞; 1]
ответ: х ∈ [-3; 1]