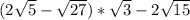тогда получается как я уже вам решал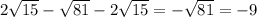
1) а) √D = √(49-4*2*(-9)) = √121 = 11
x1,2 = (-b±√D)÷2a = (-7±11)÷4
x1 = (-7+11)÷4 = 1
x2 = (-7-11)÷4 = -4,5
б) 3х² - 18х = 0
3х(х-6) = 0
3х = 0 или х-6 = 0
х1 = 0, х2 = 6
в) 100х² - 16 = 0
100х² = 16
х = √0,16 = ±0,4
х1 = -0,4; х2 = 0,4
г) х² - 16х + 63 = 0
х1 + х2 = -b; x1 × x2 = c
x1 = 9; x2 = 7
2) 2(a+b) = 20; a×b = 24
a+b = 20/2 = 10, a = 10 - b
(10-b)b = 24; b²-10b+24 = 0
b = 6; 4
ответ: 6 см и 4 см
3) х1+х2 = -p; x1 × x2 = c
x1 - 9 = -p; -9*x1 = -18
x1 = -18/-9 = 2; p = -(2 - 9) = 7
ответ: х1 = 2; р = 7
Отметь как лучший
а) у^2+12y+36=0 Лучше находить D1, если помнишь)
D=144-144=0 Значит один корень) х=-b: 2а= -6.
а=1, значит разложение выглядит таким образом =(х-(-6))=(х+6)
вроде так..сразу видно формулу сокращенного умножения (У+6)^2
б)1)Думаю, здесь проще скобки раскрыть)
сперва формула сокращенного умножения (5х-1)(5х+1)=(5х)^2-1^2=25Х^2-1
25х^2-1-(25х^2+20х+4)=0
раскроем скобки 25х^2-1-25x^2-20x-4=0 взаимно уничтожаются
-1-20х-4=0 х=-4
2)36 b ^2-121=0
опять же ссылаясь на формулы
(6b-11) (6b+11)=0
Произведение двух множителей равно нулю..
6b-11=0 6b+11=0
b=11/6 b= - 11/6
