тк 5^x положительно при любом x , то можно поделить обе часть на:
5^x не боясь за перемену знака неравенства:
(3/5)^x +(4/5)^x- 1<=0
Cумма степенных функций монотонная функция ,(тк сумма монотонных функций функция монотонная), а значит пересекает ось x в одной точке. Подбором сразу видно что x=2. При увеличении x значение функции убывает, тк 3/5<1 и 4/5<1 , таким образом решение: x>=2
ответ: x>=2
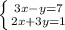
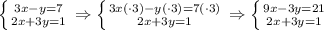
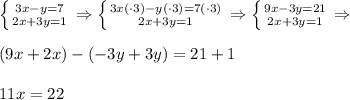
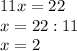
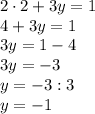
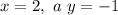
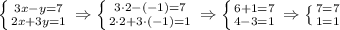
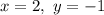
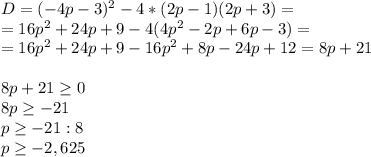
Равенство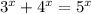 возможно только при х = 2 (т. Пифагора). Отсюда следует, что
возможно только при х = 2 (т. Пифагора). Отсюда следует, что 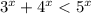 при х > 2.
при х > 2.
ответ: x ≥ 2.