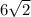Объяснение:1 Запишем
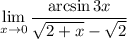2 Умножим на 1Но мы представим 1 как дробь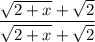 
, такое действие еще называют домножением на сопряжённое
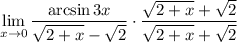
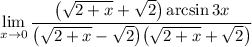
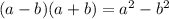где
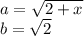
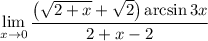
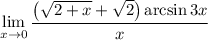
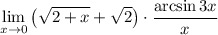7 Представим предел произведения как произведение пределов
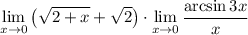8 Посчитаем первый предел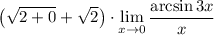
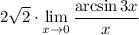9 Так как 
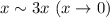то мы можем заметить в пределе 
на 
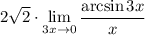10 Умножим выражение пол пределом на 1Но 1 мы представим в виде 
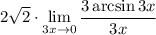
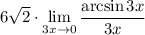
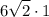ОТВЕТ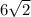
В решении.
Объяснение:
Дана функция у=√х:
а) График которой проходит через точку с координатами А(а; 83). Найдите значение а.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
83 = √а
(83)² = (√а)²
а=6889;
b) Если х∈[0; 36], то какие значения будет принимать данная функция?
у= √х
у=√0=0;
у=√36=6;
При х∈ [0; 36] у∈ [0; 6].
с) y∈ [14; 28]. Найдите значение аргумента.
14 = √х
(14)² = (√х)²
х=196;
28 = √х
(28)² = (√х)²
х=784;
При х∈ [196; 784] y∈ [14; 28].
d) Найдите при каких х выполняется неравенство у ≤ 5.
√х <= 5
(√х)² <= (5)²
х <= 25;
Неравенство у ≤ 5 выполняется при х <= 25.
Зададим коэф. к1 = - 2, к2 = 3.
Пусть первый график пройдет через точку (0;5), тогда его уравнение будет:
у = - 2х + 5, ось Оу пересечется в координате у = 5, ось Ох - в координате х = 2,5.
Чтобы второй график имел пересечение с первым, допустим, в первой четверти, нужно, чтобы выполнилось равенство у = 3х + б, где у = 0, х ∈ (0; 2,5),
на самом деле, можно еще чуть меньше 0, но точно надо посчитать.
Теперь подставим в уравнение второй функции наши значения, и решим его, чтобы определиться с б: 0 = 3*0,5 + б, б = -1,5, след., уравнение второй функции будет: у = 3х - 1,5
Можете начертить обе функции для проверки :-)