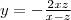
1.7546
Объяснение:
Для начала рассмотрим сферу с произвольным радиусом R и вычислим максимальный объем конуса, помещающегося в него. Очевидно, что его высота будет равна 2R-x, а радиус основания - sqrt(2Rx-x^2), где x - длина отрезка диаметра, отрезанного сегмента. Предполагая, что читатель знаком с формулой расчета объема конуса V=(pi/3) *r^2*h, где r - радиус основания, а h - высота конуса. Подставим наши значения: V=(pi/3) * x *
(2R-x)^2. Теперь наша задача сводится к оптимизации следующей функции: y=x*(2a-x)^2, где a - произвольный параметр. Стандартная процедура взятия производной, приравнивания ее к нулю, и решение уравнения относительно x, дает нам следующее значение x: x=2a/3 (знающий читатель может заметить, что существует также решение x=2a, но в нашем случае оно не подходит, так как при этом значении аргумента функция принимает значение своего минимального экстремума), (заметим также, что x меняется в пределах от 0 до 2a, иначе наша исходная задача теряет какой-либо смысл). Итак, подставим x=2R/3 в нашу формулу: V=(pi/3)*(2R/3)*(2R-2R/3)^2=(32pi*R^3)/81. Теперь осталось принять во внимание, что данный объем равен 1 литру, и посчитать радиус сферы: R=9.30525 см. Отсюда находим x=6.20350 см. Наконец, подставляем все в формулу sqrt(2Rx-x^2) и умножаем на 2, так как нам нужен диаметр: D=1.7546 дециметра