у=х^2-2х+7
Преобразуем следующим образом (прибавляем и вычитаем 4, чтобы выделить квадрат разности):
х^2-2х+7=(х^2-2х+4)-4+7=(х-2)^2+3
у=(х-2)^2+3
Графиком является парабола у=х^2 ветвями вверх, сдвинутая вверх по оси у на 3 единицы и вправо по оси х на 2 единицы.
Т.е. вершина имеет координаты (2;3).
Если на координатной плоскости нужно построить график только одной функции, то удобно сначала построить график у=х^2, а потом сдвинуть оси в противоположных направлениях: ось х сдвинуть на 3 единицы вниз, а ось у - на 2 единицы влево.
ну смотри.
Возьмём в пример это:
(а+4)(6+а)
Мы должны умножать дугой: а×6=6а, а×а=а², 4×6=24, 4×а=4а.
Я прикреплю фото, чтобы было понятнее.
ответом будет являться: 6а+а²+24+4а.
Но ответ не окончательный, убираем подобные: 6а и 4а.
ответ: 10а+а²+24.
Выражение в виде произведения многочленов.
Пример:
а(m-3)+b(m-3)
В данном случае общим множителем является многочлен m-3. Поэтому выносим его в начало, а множители за скобками складываем и умножаем;
(m-3)(a+b)
Метод группировки.
Метод группировки - это разложение многочлена на множители, объединив в группы его члены.
Пример:
2ас+2bc+5am+5bm
Сгруппировать члены этого многочлена нужно так, чтобы слагаемые в каждой группе имели общий множитель.
2ас+2bc+5am+5bm=(2ac+2bc)+(5am+5bm)=
=2c(a+b)+5m(a+b)=(a+b)(2c+5m).
Ничего сложного нет, нужно это только понять.)
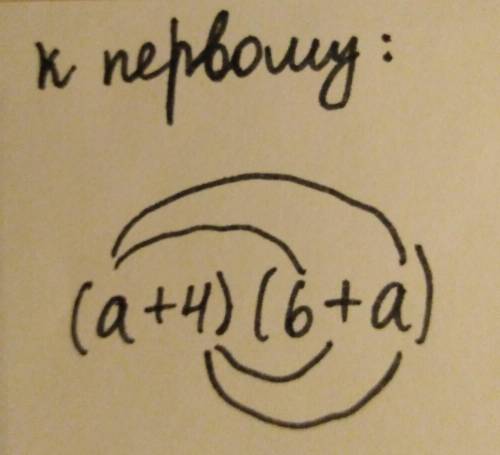
(√x)²=11²
x=121