Найдём координаты вектора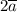 
. Для этого все координаты вектора 
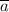нужно умножить на 2:
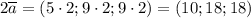
По такому же принципу найдём координаты вектора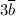 
:
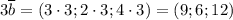
Чтобы найти координаты вектора 
, вычтем соответствующие координаты:
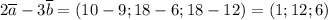
Длина произвольного вектора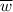 
вычисляется по формуле 
:
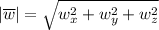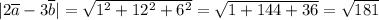
ответ: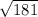 
.
***
Координаты середины отрезка есть среднее арифметическое координат конца отрезка:
***
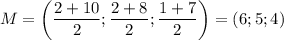
По условию точка 
делит сторону 
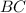пополам (и так же с двумя другими точками). Найдём координаты точки
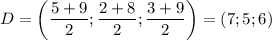
Расстояние между точкам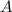и 
и 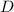(т. е. длина медианы) равно:
То есть 
.
То же самое проделаем с двумя другими медианами:
- - - - - - -
***
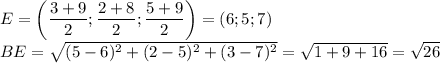
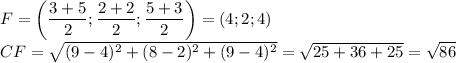
Если что-либо будет непонятно — спрашивайте.
Объяснение:
1)Найди решение неравенства. Начерти его на оси координат.
x>4.
На числовой оси отметить ноль по центру, от нуля вправо отложить четыре клеточки, это будет точка х=4. Теперь от этой точки штриховать вправо, как бы до + бесконечности. Неравенство строгое, поэтому точка 4 должна обозначаться маленьким кружком, пустым внутри.
ответ: x∈(4;+∞]
2)Отобрази решение неравенства 1≤z на оси координат. Запиши ответ в виде интервала.
На числовой оси отметить ноль по центру, от нуля вправо отложить одну клеточку, это будет точка z=1, от этой точки влево штриховать, как бы до - бесконечности.
Интервал: z ∈(-∞, 1)
⦁ Длины сторон треугольника обозначены как a, b и c. Какие из неравенств неверны?
Неясное задание.
3) Известно, что b>c.
Выбери верные неравенства:
7,9−b>7,9−c
−7,9b<−7,9c
7,9b>7,9c
b+7,9>c+7,9
b−7,9>c−7,9
Выделены верные неравенства.
x³+4x²-3x=2
x(x²+4x-3)=2
x=2 x²+4x-3=2
x²+4x-3-2=0
x²+4x-5=0
D=16+20=36=6²
x1=-4+6/2=1
x2=-4-6/2=-5
ответ:2;1;-5