Окружность с центром в т. O и D = 68. Хорда AB.
Расстояние OM = 30 от т. O до прямой AB.
Найти:AB - ?
Решение:Заметим, что OM ⊥ AB (так как OM - это расстояние от т. О до прямой AB - длина перпендикуляра из точки О к прямой AB).
Пусть отрезок OM лежит на радиусе OC рассматриваемой окружности. Тогда OC, как радиус, перпендикулярный хорде, пересекает эту хорду ровно в ее середине: AM = BM.
Рассмотрим прямоугольные треугольники, равные по первому признаку (или же по двум катетам OM = OM и AM = BM): ΔAOM = ΔBOM.
OA = OB = D / 2 = 68 / 2 = 34, как радиусы.
OM = 30, по условию.
Применим теорему Пифагора, например, к ΔAOM:
AM² + OM² = AO²
AM² = AO² - OM²
AM² = 34² - 30²
AM² = 256
AM = 16
Значит:
AB = AM + BM = AM + AM = 16 + 16 = 32.
Задача решена!
ответ: 32.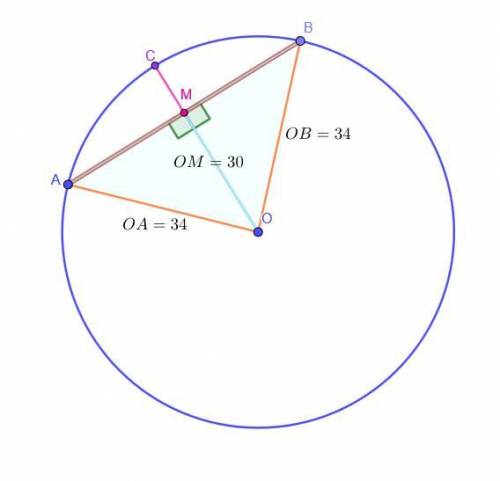
наибольшее значение многочлена равно 5.
Объяснение:
- 9х² + 12х + 1
- (9х² - 12х - 1) = - ((3х)² - 2·3х·2 + 2² - 5) = -((3х - 2)² - 5) = - (3х - 2)² + 5.
Второе слагаемое 5 неизменно, поэтому наибольшего значения вся сумма достигнет тогда, когда наибольшим будет первое слагаемое - (3х - 2)².
(3х - 2)² ≥ 0 при любом действительном значении х, тогда
- (3х - 2)² ≤ 0, а значит наибольшим его значением является 0.
Получили, что в этом случае сумма будет равной 0 + 5 = 5, и это и есть наибольшее значение многочлена 1+12x-9x².
Рассмотрим функцию у = 1+12x-9x².
Она квадратичная, графиком является парабола. Так как а = - 9, а < 0, то ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы.
х вершины = -b/(2a) = -12/(-18) = 2/3.
у вершины = 1 + 12·2/3 - 9·4/9 = 1 + 8 - 4 = 5.
у=5-4х/3