Объяснение:
1.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч). ⇒
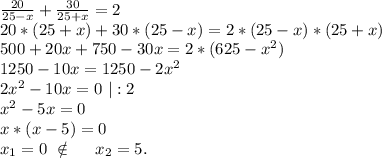
ответ: скорость течения реки 5 км/ч.
2.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч).
Пусть время, затраченное на путь против течения реки равно t₁, а
а время, затраченное на путь по течению реки равно t₂. ⇒
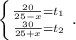
Суммируем эти уравнения:

По условию задачи на весь путь катер затратил t₁+t₂=2 (ч). ⇒
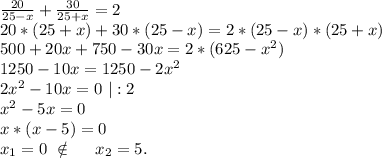
ответ: скорость течения реки 5 км/ч.
1. Пусть равное количество окуней равно х. ⇒
2. Первый рыболов поймал х+7,второй х+6, а третий х+8.
3. (x+7)+(x+6)+(x+8)=51
3x+21=51
3x=30 |:3
x=10 ⇒
ответ: первый рыболов поймал 17 окуней,
второй рыболов поймал 16 окуней,
третий рыболов поймал 18 окуней.
Объяснение:
1.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч). ⇒
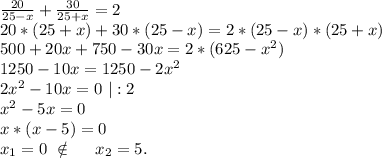
ответ: скорость течения реки 5 км/ч.
2.
Пусть скорость течения реки равна х. ⇒
Против течения реки скорость катера будет равна 25-х (км/ч),
а по течению реки скорость катера будет равна 25+х (км/ч).
Пусть время, затраченное на путь против течения реки равно t₁, а
а время, затраченное на путь по течению реки равно t₂. ⇒
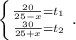
Суммируем эти уравнения:

По условию задачи на весь путь катер затратил t₁+t₂=2 (ч). ⇒
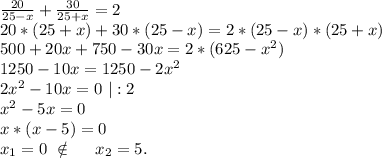
ответ: скорость течения реки 5 км/ч.
1. Пусть равное количество окуней равно х. ⇒
2. Первый рыболов поймал х+7,второй х+6, а третий х+8.
3. (x+7)+(x+6)+(x+8)=51
3x+21=51
3x=30 |:3
x=10 ⇒
ответ: первый рыболов поймал 17 окуней,
второй рыболов поймал 16 окуней,
третий рыболов поймал 18 окуней.
S=2*(V+10) скорость автобуса увеличилась на 10, время стало 2ч
2,5*V=2*(V+10)
2.5V-2V=20
0.5V=20
V=20/0.5
V=40км/ч скорость
S= 2.5*40=100 км расстояние