Косинус угла равен 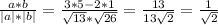
Угол равен 45 градусов.
Задание 1: По свойству интеграла, можем расписать: ∫4x^3dx - ∫2dx + ∫cos2xdx ; ответ: x^4-2x + sin2x/2 + C
∫cos2xdx = {t = 2x; t' = 2}(Подставить дифференциал, использую dx=1/t' *dt) = ∫cost/2dt = 1/2∫costdt = 1/2*sint = sin2x/2(Взяли замену 2х за t и возвращаем назад)
Задание 2: Здесь использую интегрирование по частям: ∫u dv = uv - ∫v du, отсюда замену возьмем {u =4x+5; dv=cos4x dx}; Нужно найти дифференциал du, используя du = u' d, а v вычисляем с и подставить du = 4dx и v = sin4x/4; Получаем: (4x+5)*(sin4x/4)- ∫(sin4x/4)*4dx; ∫sin4x/4dx = {t = 4x; t' =4} = ∫sin4x * 1/4 dt = ∫sint/4 dt (Также, как и впервой задаче с cos);
(4x+5)*(sin4x/4) - 1/4∫sin(t)dt; (4x+5)*(sin4x/4)-1/4*(-cos(t)); Делаем возврат t на 4х; ответ: ((4x+5)*sin(4x)+cos(4x))/4 + C
Задание 3: Делаю замену {t = cosx; t' =-sinx} = -∫t^5 dt (Подставить дифференциал, использую dx=1/t' *dt) = -t^6/6 + C, делаю возврат t = cosx и ответ будет -(cos^6(x)/6) + C
cosα=a*b/|a|*|b|=13/√13*√26=13/13*√2=1/√2=√2/2;
α=arccos(√2/2)=π/4=45°.
ответ: 45°.