<!--c-->
Во всех ситуациях используем перестановки.
Перестановки — это специальный случай размещений, когда выборка так же велика, как данное множество.
Размещения по n элементов из n называются перестановками из n элементов.
Вычисляя перестановки, определяется, сколькими различными можно переупорядочить элементы множества, не меняя их количество.
Количество перестановок обозначается как Pn, где n — количество элементов множества.
Перестановки вычисляются по формуле Pn=n!=1⋅2⋅...⋅n.
1. Так как Игнат и Николай финишируют друг за другом, то оба ученика могут финишировать двумя Игнат - Николай и Николай -Игнат.
И, если один из них финиширует первым, то остальные участники, которых осталось 15−2=13, и второй мальчик могут финишировать 13+1=14! различными
Далее используем правило произведения:
Если элемент A можно выбрать и затем второй элемент B можно выбрать m различными то пару элементов A и B можно выбрать
В результате получим 2⋅14! различных
2. По условию Вадим может занять любое из 13 мест, кроме первого и последнего.
Остальные участники могут финишировать 15−1=14! различными
Так как заданые два события произходят одновременно, то далее используем правило произведения:
Если элемент A можно выбрать и затем второй элемент B можно выбрать m различными то пару элементов A и B можно выбрать
Получим 13⋅14! различных
(см. объяснение)
Объяснение:
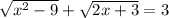
Введем функцию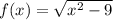 
.
Найдем D(f):
![x^2-9\ge0\\x\in(-\infty;\;-3]\cup[3;\;+\infty)](/tpl/images/1431/8237/ead74.png)
Т.к. корень не меняет монотонность функции, то на промежутке ![(-\infty;\;-3]](/tpl/images/1431/8237/54e60.png)
функция 
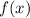убывает, а на промежутке 
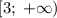возрастает.
Введем функцию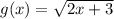 
.
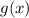монотонно возрастает на промежутке 
.
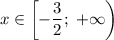Т.к. все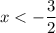 
не подходят по ОДЗ для 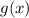, а часть функции 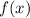, определенная на промежутке 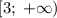, возрастает, то имеем сумму возрастающих функций, а значит 
возрастающая.
Значит уравнение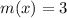 
имеет единственный корень.
Предположим, что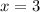 
- корень уравнения.
Проверим это:
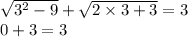
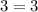, верно.
Значит 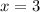- это корень исходного уравнения.
Поэтому правильный ответ на задание 3) 3.
Уравнение решено!
5х=90
х=18
вроде так