В решении.
Объяснение:
Скорость моторной лодки в стоячей воде 7 км/ч. Время, затраченное на движение лодки на 24 км по течению и на 24 км против течения равно 7 часам. Найти скорость течения реки.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость течения реки.
7 + х - скорость лодки по течению.
7 - х - скорость лодки против течения.
24/(7 + х) - время лодки по течению.
24/(7 - х) - время лодки против течения.
По условию задачи уравнение:
24/(7 + х) + 24/(7 - х) = 7
Умножить все части уравнения на (7 - х)(7 + х), чтобы избавиться от дробного выражения:
24*(7 - х) + 24*(7 + х) = 7*(7 - х)(7 + х)
168 - 24х + 168 + 24х = 343 - 7х²
7х² = 343 - 336
7х² = 7
х² = 1
х = √1
х = 1 (км/час) - скорость течения реки.
Проверка:
24/ 8 + 24/6 = 3 + 4 = 7 (часов), верно.
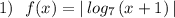
Сначала строим график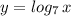 
, затем сдвигаем его на 1 единицу влево вдоль оси ОХ, получаем график функции 
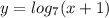. А потом отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график заданной функции 
.
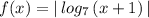Как видно из графика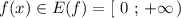 
. См. рис.
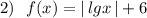
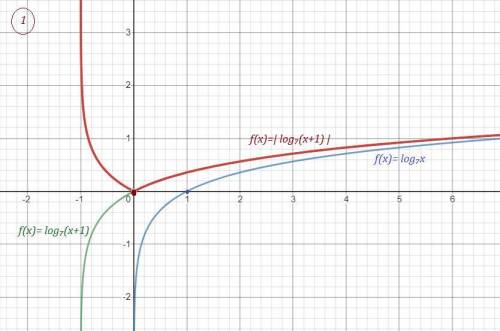
Сначала строим график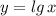 
, затем отображаем ту часть графика, которая лежит ниже оси ОХ , в верхнюю полуплоскость и получим график функции 
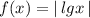. Потом смещаем этот график на 6 единиц вверх вдоль оси ОУ , получим график заданной функции .
Как видно из графика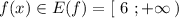 
. См. рис.
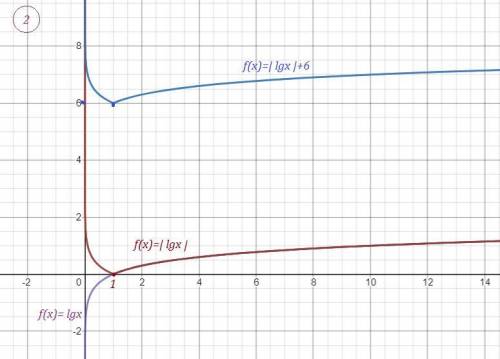
1.
x²-x>0
x(x-1)>0
x=0 ∨ x=1
x∈(-∞,0)u(1,∞)
2.
2x+x²<0
x(2+x)<0
x=0 ∨ x=-2
x∈(-2,0)
3.
x²-3x>0
x(x-3)>0
x=0 ∨ x=3
x∈(-∞,0)u(3,∞)
4.
5x+x²<0
x(5+x)<0
x=0 ∨ x=-5
x∈(-5,0)
5.
x²-4>0
x²>4
x>2 ∨ x<-2
x∈(-∞,-2)u(2,∞)
6.
x(x²-9)<0
x(x-3)(x+3)<0
x=0 ∨ x=3 ∨ x=-3
x∈(-∞,-3)u(0,3)