Проболела тему. объясните и с . тема: степень с натуральным показателем. степень и её свойства. : вычислите: а)сумму кубов чисел 5 и -3. б) куб суммы чисел 9 и - 11. в)разность квадратов чисел 12 и 8. г)квадрат разности чисел 12 и 8. д) удвоенное произведение квадратов чисел 7 и -5 е) утроенное произведение числа 15 и квадрата числа 4. объясните тему. 35 .
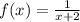


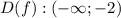 ∪
∪
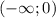 ∪
∪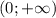

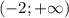
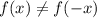
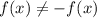

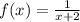


 ∪
∪
 ∪
∪

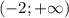
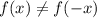
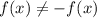


Степень с натуральным показателем и её свойстваСтепень с натуральным показателем и ее свойства.Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен a:an = В выражении an :- число а (повторяющийся множитель) называют основанием степени- число n (показывающее сколько раз повторяется множитель) – показателем степениНапример:
25 = 2·2·2·2·2 = 32,
здесь:
2 – основание степени,
5 – показатель степени,
32 – значение степениОтметим, что основание степени может быть любым числом.Вычисление значения степени называют действием возведения в степень. Это действие третьей ступени. То есть при вычислении значения выражения, не содержащего скобки, сначала выполняют действие третьей ступени, затем второй (умножение и деление) и, наконец, первой (сложение и вычитание).Для записи больших чисел часто применяются степени числа 10. Так, расстояние от земли до солнца примерно равное 150 млн. км, записывают в виде 1,5 · 108Каждое число большее 10 можно записать в виде: а · 10n , где 1 < a < 10 и n – натуральное число. Такая запись называется стандартным видом числа.Например: 4578 = 4,578 · 103 ;103000 = 1,03 · 105.Свойства степени с натуральным показателем:1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываютсяam · an = am + nнапример: 71.7 · 7 - 0.9 = 71.7+( - 0.9) = 71.7 - 0.9 = 70.82. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаютсяam / an = am — n ,где, m > n,a ? 0например: 133.8 / 13 -0.2 = 13(3.8 -0.2) = 133.63. При возведении степени в степень основание остается прежним, а показатели степеней перемножаются.(am )n = a m · nнапример: (23)2 = 2 3·2 = 264. При возведении в степень произведения в эту степень возводится каждый множитель(a · b)n = an · b m ,например:(2·3)3 = 2n · 3 m ,5. При возведении в степень дроби в эту степень возводятся числитель и знаменатель(a / b)n = an / bnнапример: (2 / 5)3 = (2 / 5) · (2 / 5) · (2 / 5) = 23 / 53
а) 5³ + -3³=98
б)(9+ -11)³=-8
в)12²-8²=208
г)(12-8)²=16
д)2*(7²*-5²)=-2450
е)(14*4²)*3=672