Запишите многочлен 4- ой степени, корнями которого являются числа :
если число а-корень уравнения то х-а=0
воспользовавшись этим свойством составим уравнения
1) - 2,0,2,3
(x+2)(x-0)(x-2)(x-3)=0
x(x-2)(x+2)(x-3)=0
x(x²-4)(x-3)=0
(x²-4)(x²-3x)=0
перемножим скобки
x⁴-4x²-3x³+12x=0
приведем к стандартному виду
x⁴-3x³-4x²+12x=0
2) - 3,-1,1,3
(x+3)(x+1)(x-1)(x-3)=0
(x²-9)(x²-1)=0
x⁴-9x²-x²+9=0
x⁴-10x²+9=0
3) - 3,-1,0,3
(x+3)(x+1)(x-0)(x-3)=0
(x²-9)*x*(x+1)=0
(x²-9)(x²+x)=0
x⁴-9x²+x³-9x=0
x⁴+x³-9x²-9x=0
4) -2,1,2,5
(x+2)(x-1)(x-2)(x-5)=0
(x²-4)(x-1)(x-5)=0
(x²-4)(x²-6x+5)=0
x⁴-4x²-6x³+24x+5x²-20=0
x⁴-6x³+x²+24x-20=0
1) π / 4, π / 4, π / 2;
2) π / 3, π / 3, π / 3;
3) π / 2, π / 2, π / 2, π / 2.
Для того, чтобы решить задачу, нужно знать, что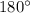
соответствует 
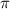радианам.1 ) Углы равнобедренного прямоугольного треугольника равны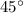 
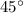, и 
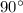(если треугольник "прямоугольный", то в нем есть угол в 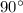, а если к тому же равнобедренный, то его два оставшихся угла равны по 
).
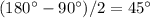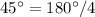, откуда каждый из углов треугольника в 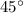равен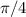 
радиан.
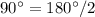, или же 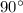- это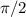 
радиан.
2 ) Сумма углов треугольника равна 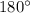или 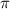радианам. Если треугольник равносторонний (название говорит само за себя), то все его три угла равны. Иначе говоря, каждый из них равен 
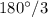(что равно 
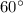) или же 
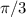радиан.
3 ) Все углы прямоугольника (таковых имеется четыре) равны. А сумма углов прямоугольника, как и любого четырехугольника, равна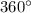 
, что равняется 
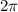радиан. Отсюда несложно сделать вывод, что каждый из углов прямоугольника равен 
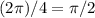радиан.
Или можно вспомнить, что с углом в 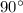мы уже встречались в первом пункте задачи: как было выяснено, он соответствует 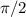радиан.
Д=в²-4ас=-2²-4*(-1)*15=4+60=64
х1=
x2=