41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
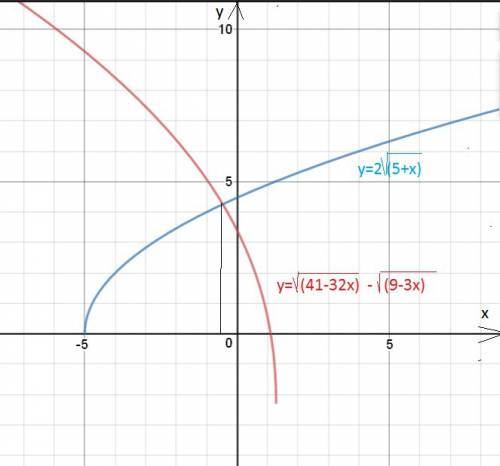
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
4*2^[x] - 4*2^[-x] = 15
4*2^[x] - 4/2^[x]=15
Пусть 2^[x]=t (t>0), получаем исходное уравнение
4t-4/t=15
4t^2-15t-4=0
D=(-15)²-4*4*(-4)=289; √D=17
t1=-0.25 - не удовлетворяет усл.
t2=4
Возвращаемся к замене
2^[x]=4
2^[x]=2^[2]
x=2
ответ: 2.