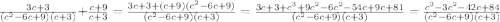Объяснение:
1). y²-y-12=0; D=1+48=49
y₁=(1-7)/2=-6/2=-3
y₂=(1+7)/2=8/2=4
ответ: -3; 4.
2). 5x²+10x-15=0 |5
x²+2x-3=0; D=4+12=16
x₁=(-2-4)/2=-6/2=-3
x₂=(-2+4)/2=2/2=1
ответ: -3; 1.
3). -x²-8x+9=0 |×(-1)
x²+8x-9=0; D=64+36=100
x₁=(-8-10)/2=-18/2=-9
x₂=(-8+10)/2=2/2=1
ответ: -9; 1.
4). Видимо в условии было дано такое выражение:
5y²+2y-3=0; D=4+60=64
y₁=(-2-8)/10=-10/10=-1
y₂=(-2+8)/10=6/10=0,6
ответ: -1; 0,6.
5). y²+9y+18=0; D=81-72=9
y₁=(-9-3)/2=-12/2=-6
y₂=(-9+3)/2=-6/2=-3
ответ: -6; -3.
Объяснение:
Рассмотрим числа x y z:
1) Если все положительные x y z, то и результат будет положительный.
2) Если одно из значений отрицательно, то каждая дробь будет отрицательной и ответ будет отрицательный:
К примеру возьмём x=10, y=10, z=-10
3)Если два отрицательных, то ответ будет положительным (аналогично 2 примеру)
4)и наконец 3 отрицательных, все дроби отрицательные⇒ответ отрицательный.
Т.к. наше выражение =3>0, то нас устраивают случаи 1) и 3).
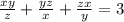
Преобразуем равенство, умножив на 2xyz(x,y,z≠0):
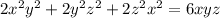
5) Отсюда видно что если числа x, y, z являются решением, то, изменив знак у любых двух чисел из этой тройки, мы снова получим решение уравнения. Поэтому достаточно рассмотреть положительные решения, а оставшиеся получить путем чередования двух минусов.
Рассмотрим левую часть уравнения:
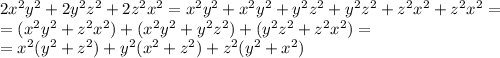
Помним, что квадрат числа неотрицательное число, поэтому:
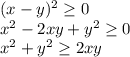
Значит наше выражение:
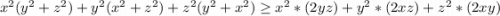
Вспомним что изначальное выражение равнялось 6xyz:
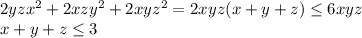
Т.к. x,y,z положительные, то в натуральных числах есть одно решение: (1,1,1).
Учитывая 5 пункт получаем 4 решения:
(1,1,1), (-1;-1;1), (-1;1;-1), (1;-1;-1)
Объяснение:
Это задание в первую очередь ориентировано на проверку ваших знаний ФСУ или Формул Сокращённого Умножения.
Давайте просканируем пример на их наличие.
1.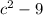 - Это разность квадратов, а именно квадрата числа с и числа 3. Возможно вы зададите резонный вопрос - а зачем нам это отслеживать. В работе с дробями важно уметь находить взаимосвязи между знаменателями.
- Это разность квадратов, а именно квадрата числа с и числа 3. Возможно вы зададите резонный вопрос - а зачем нам это отслеживать. В работе с дробями важно уметь находить взаимосвязи между знаменателями. 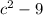 раскладывается рак (с-3)(с+3)
раскладывается рак (с-3)(с+3)
2.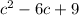 - знаменатель второй дроби и является квадратом разности(смотрим по знаку перед вторым числом). Он раскладывается как (с-3)(с-3).
- знаменатель второй дроби и является квадратом разности(смотрим по знаку перед вторым числом). Он раскладывается как (с-3)(с-3).
Что-то напоминает не так ли? Таким образом, с-3 это общий множитель обоих знаменателей. Значит нужно перемножит каждую дробь на оставшийся общий множитель другой дроби
Я специально оставила дробь полностью раскрытой, т.к. она нам ещё может понадобиться.
3.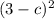 - аналогично пункту 2 квадрат разности. Раскладывается практически аналогично. Но т.к. от перемены мест слагаемых сумма не меняется это исправимо.
- аналогично пункту 2 квадрат разности. Раскладывается практически аналогично. Но т.к. от перемены мест слагаемых сумма не меняется это исправимо.
Дальше приведём получившуюся дробь и оставшуюся к общему знаменателю.