![\int \frac{cos^2xdx}{sin^4x}=\int \frac{cos^2x}{sin^2x}\cdot \frac{dx}{sin^2x}=\int ctg^2x\cdot \frac{dx}{sin^2x}=[t=ctgx,\; dt=-\frac{dx}{sin^2x}]=\\\\=-\int t^2\cdot dt=-\frac{t^3}{3}+C=-\frac{ctg^3x}{3}+C\\\\\\\int \frac{dx}{cos^4x\cdot sin^2x}=\int \frac{\frac{dx}{cos^6x}}{\frac{cos^4xsin^2x}{cos^6x}}=\int \frac{(\frac{1}{cos^2x})^2\cdot \frac{dx}{cos^2x}}{tg^2x}=\\\\=[t=tgx,dt=\frac{dx}{cos^2x},1+tg^2x=\frac{1}{cos^2x}]=\int \frac{(1+t^2)^2dt}{t^2}=\int \frac{1+2t^2+t^4}{t^2}dt=](/tpl/images/0322/2276/4cbe9.png)
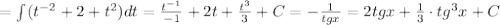
Объяснение:
Решая 6- задания, Юрий ежеминутно зарабатывает:
: 6 минут =
При решении 8- заданий, Юрий ежеминутно зарабатывает:
: 9 минут = 8/
а при решении 10- задач:
: 15 минут = 10/15 = 2/
Таким образом, в течение 45 минут максимальное количество может быть получено при решении максимально возможного количества 6- заданий, а в оставшееся время - 8- заданий.
Пусть х - количество 6- заданий, у - количество 8- заданий, тогда лимит времени, которым располагает Юрий, равен:
6·х + 9·у = 45 минут
Так как 6х не кратно 45, то принимаем у = 1 (минимальное значение 8- заданий), тогда х = (45 - 9) : 6 = 36 : 6 = 6 заданий.
Следовательно, наибольшее количество , которое может набрать Юрий за первые 45 минут работы, равно:
6 · 6 + 8 · 1 = 36 + 8 =
ответ:
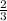от того, что осталось после первого деня, то после второго дня работы осталась 
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
