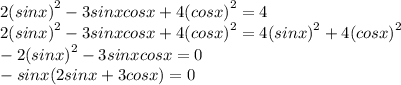
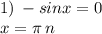
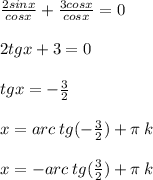
ответ:: S6 = 10,2
Объяснение:
1. Для определения суммы шести членов арифметической прогрессии необходимо узнать значение шестого ее члена и только тогда найти S6 по формуле
Sn = (a1 + an) : 2 * n.
2. Известна формула для энного члена арифметической прогрессии
аn = a1 + d *(n - 1).
3. Пользуясь этой формулой вычислим разность прогрессии d.
a4 = a1 + d * 3;
1,8 = 1,2 + 3 d;
d = (1,8 - 1,2) : 3 = 0,6 : 3 = 0,2.
4. Теперь найдем а6.
а6 = а1 + d * 5 = 1,2 + 0,2 * 5 = 1,2 + 1 = 2,2.
5. Отвечаем на во задачи
S6 = (a1 + a6) : 2 * 6 = (1,2 + 2,2) : 2 * 6 = 10,2.
Во слишком много - ответы тоже краткие.
Объяснение:
1,1 f(-6) = 1/3*36 +12 = 24 - ответ.
1.2 f(2) = 1/3*4 - 2*2 = - 2 2/3 - ответ
2. Не допускается деление на 0.
Дано: y =x²-1*x-6 - квадратное уравнение.
Вычисляем дискриминант - D.
D = b² - 4*a*c = (-1)² - 4*(1)*(-6) = 25 - дискриминант. √D = 5.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (1+5)/(2*1) = 6/2 = 3 - первый корень
x₂ = (-b-√D)/(2*a) = (1-5)/(2*1) = -4/2 = -2 - второй корень
3 и -2 - корни уравнения - исключить из ООФ.
D(f) = R\{-2;3} = (-∞;-2)∪(-2;3)∪(3;+∞) - ответ
3,1
Дано: y = x²-4*x+3 - квадратное уравнение.
D = b² - 4*a*c = (-4)² - 4*(1)*(3) = 4 - дискриминант. √D = 2.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (4+2)/(2*1) = 6/2 = 3 - первый корень
x₂ = (-b-√D)/(2*a) = (4-2)/(2*1) = 2/2 = 1 - второй корень
3 и 1 - нули функции.
Минимум посередине между нулями = (1+3)/2 = 2 = x.
Fmin(2) = -1
Вершина параболы в точке А(2;-1), ветви вверх.
1) E(f) = [-1;+∞) - область значений.
2) Убывает: х = (-∞;2)
3) Положительна при Х=(-∞;1)∪(3;+∞) - ответ
4) Графики на рисунке в приложении.
5) Разрывы при делении на 0 в знаменателе.
х² ≠ 16 и х ≠ ± 4.
D(f) = R\{-4;4} = (-∞;-4)∪(-4;4)∪(4;+∞) - ответ.
Произведение равно нулю, если хотя бы один из множителей равен нулю
Разделим левую и правую части уравнения на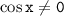 , получим:
, получим: