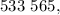которая должна выражать дату (в каком-то неизвестном представлении).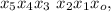
;
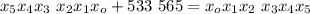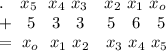
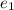– возможная добавочная единица, уходящая из первого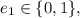
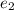– возможная добавочная единица, уходящая из второго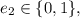
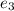– возможная добавочная единица,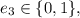
;
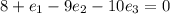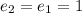и при 
;
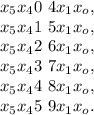
поскольку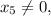 
так как с этой цифры начинается разностное число.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.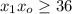
.
.
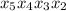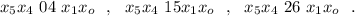
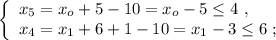
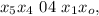
может играть роль апреля.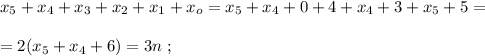
;
;
;
;
;
;
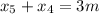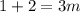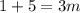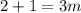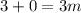– дата 12/04/56 г.
– дата 15/04/86 г.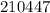
– дата 21/04/47 г.
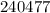– дата 24/04/77 г.
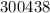– дата 24/04/38 г.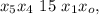
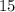может играть только роль числа месяца (дня).
;
;
;
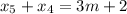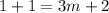– дата 11/15/46 г.
а - первое число арифметической прогрессии
b - второе число арифметической прогрессии
c - третье число арифметической прогрессии
а+b+с = 9 -сумма членов ариф. прогрессии
Сумму членов ариф. прогрессии можно вычислить и по формуле
Sₓ = ((а+с)/2) * х
где х = 3 - количество членов ариф. прогрессии
S₃ = ((а+с)/2) *3 = 9
((а+с)/2) *3 = 9
((а+с)/2) = 9/3 =3
(а+с) = 3*2
а+с = 6
определим b - второй член ариф. прогресс.
а+b+с = 9
b = 9-а-с = 9-6 = 3 -второй член ариф. прогресс.
по условию задачи
(а + 1) - первое число геометрической прогрессии
(b + 1) - второе число геометрической прогрессии
(с + 3) - третье число геометрической прогрессии
(а + 1) * (b + 1) * (с + 3) геометр. прогрессия
где b + 1 = 3+1 = 4 второй член геометр. прогрессии
второй член. геом. прогрессии вычисляется по формуле b₂=b₁*q ( где q - знаменатель геом. прогрессии)
следовательно:
b = (а+1) * q
4 = (а+1) * q
q = 4/(а+1)
выразим третий член геом. прогрессии (с + 3) по формуле b₃=b₂*q
(с + 3) = 4*q (подставим в формулу значение q = 4/(а+1))
с+3 = 4*4/(а+1)
с+3 = 16/(а+1)
с = (16/(а+1)) - 3общий знаменатель (а+1)
с = (16-3а-3) / (а+1)
с=(13-3а) / (а+1)
подставим значение с в формулу а+с = 6 (смотри в начале решения)
а + ((13-3а) / (а+1)) = 6 ---левую часть под общий знаменатель (а+1)
(а*(а+1) +13-3а) / (а+1) = 6
а² + а + 13 - 3а = 6*(а+1)
а²-2а+13 = 6а +6
а² - 8а + 7 = 0отсюда находим а = 1 - первый член ариф. прогр.
проверка1²- 8*1 + 7 = 0
т. к. а+с = 6, значит с = 6-а=6-1 = 5 - третий член ариф. прогрессии
итого: а = 1 - первый член ариф. прогр.
b=3 - второй член ариф. прогресс.
с = 5 - третий член ариф. прогрессии
проверка: а+b+с = 1+3+5= 9 -верно
(а + 1)=1+1 = 2 - первое число геометрической прогрессии
(b + 1) =3+1 = 4 - второе число геометрической прогрессии
(с + 3)=5+3 = 8 - третье число геометрической прогрессии
q = 4/(а+1) = 4/(1+1)= 2 -знаменатель геом. прогрессии
проверка: 2*2=44*2=8верно
решение представлено на фото
Объяснение: