97,5
Объяснение:
Данная задача решаема через систему уравнения:
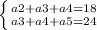
Решим эту систему при метода вычитания:
a3+a4=18-a2
a3+a4+24-a5
24-a5=18-a2
6-a5+a2=0
a5-a2=6 - данное выражение показывает нам разницу между членами прогресcии через a3 и a4
Разница между ближайшими членами d = 1,5 ,потому-что согласно a5-a2=6
Теперь есть формула:
a2=a1+d => d=1,5 => a2=a1+d ,тогда подставим в первое уравнение системы:
a1+1,5+a3+a4=18
Но при этом а3=a1+3 и а4=а1+4,5
Тогда:
a1+1,5+a1+3+а1+4,5=18
3*a1+9=18
a1=3
Находим все члены и их сумма равна:
3+4,5+6+7,5+9+10,5+12+13,5+15+16,5=97,5
ответ: 97,5
(В решении или в вычислениях могу ошибаться!)
Угадываем корни 2 и - 2. Заметим, что 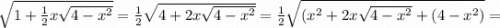
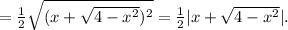 ОДЗ:
ОДЗ: ![x\in[-2;2].](/tpl/images/2015/3850/be6a3.png) Пытаемся доказать, что других корней нет.
Пытаемся доказать, что других корней нет.
1)  уравнение принимает вид
уравнение принимает вид



Исследуем знак второй производной: f''(x)=0 - когда  где
где
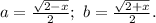 Поскольку a³≤a², b³≤b², причем при a∈(0,1); b∈(0,1) неравенства строгие, делаем вывод, что такое возможно только при a=1; b=0 или a=0; b=1, при прочих a и b, удовлетворяющих второму уравнению, сумма их кубов будет меньше 1, откуда вторая производная всюду неотрицательна, то есть функция вогнута. А поскольку
Поскольку a³≤a², b³≤b², причем при a∈(0,1); b∈(0,1) неравенства строгие, делаем вывод, что такое возможно только при a=1; b=0 или a=0; b=1, при прочих a и b, удовлетворяющих второму уравнению, сумма их кубов будет меньше 1, откуда вторая производная всюду неотрицательна, то есть функция вогнута. А поскольку  других решений на промежутке
других решений на промежутке![[-2,-\sqrt{2}]](/tpl/images/2015/3850/41969.png) нет.
нет.
2)  уравнение принимает вид
уравнение принимает вид
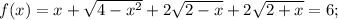
На этом участке подобное рассуждение не проходит; кроме x=2 точно есть корень слева от нуля, поскольку f(0)>6. Будем рассуждать иначе.
![a=\sqrt{2-x}\ge0;\ b=\sqrt{2+x}\ge 0;\ a^2+b^2=4; b=2\cos t; a=2\sin t; t\in [0;\frac{\pi}{2}];](/tpl/images/2015/3850/dd94a.png)
 уравнение превращается в
уравнение превращается в

Обе части положительны, смело возводим в квадрат (а можно было и к половинному углу свести):

6-6cos 2t-10sin 2t+2sin 2t cos 2t=0;
12sin² t-20 sin t cos t+4sin t cos t(cos² t-sin² t)=0; sin t=0 (⇒ a=0; b =2; x=2) или 3 sin t-5cos t+cos³ t-cos t sin² t=0;
(3sin t-5cos t)(cos²t+sin²t)+cos³ t-cos t sin^2 t=0;
3sin³t-6sin²t cos t+3sin t cos²t-4cos³ t=0; очевидно cos t≠0; tg t=p;
3p³-6p²+3p-4=0; домножаем на 9 и замена 3p=q: q³-6q+9q-36=0;
(q-2)³-3(q-2)-34=0; 

![q-2=\sqrt[3]{17\pm12\sqrt{2}}+\frac{1}{\sqrt[3]{17\pm12\sqrt{2}}};](/tpl/images/2015/3850/dad89.png) но
но ![\sqrt[3]{17+12\sqrt{2}}\cdot \sqrt[3]{17-12\sqrt{2}}=1\Rightarrow](/tpl/images/2015/3850/0cfe0.png)
![q=2+\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}};\ p=\frac{2+\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}}}{3};](/tpl/images/2015/3850/e95cc.png)

Вот этот корень мы и искали. Подставлять найденное p для выписывания b, а затем x, сил уже не осталось.
Возможно, я где-то ошибся, но ошибку пока не вижу. Засим разрешите откланяться.
б) 2√7 * √21 = 2√7 * 7 * 3 = 2*7*√3 = 14√3
в) = 2√2 * √2 - √50 * √2 = 2*2 - √100 = 4 - 10 = -6
г) = 4√80/5 - √125/5 = 4√16 - √25 = 4 * 4 - 5 = 16-5=11
д) =6√x -2/3 * 3√x +10*1/2 * √x = 6√x-2√x+5√x = 9√x
е) = √ab/b + √b/b = √a + 1