(1/a-1/b)*((a+b)^2-a^2-b^2)/(a-b)^2)=
(1/a-1/b)*((a^2+2ab+b^2-a^2-b^2)/(a-b)^2)=
((1/a-1/b)*(2ab/(a-b)^2)=
((b-a)/ab)*(2ab/(a-b)^2)=
(-(a-b)/ab) *(2ab/(a-b)^2)=
-2/(а-b) =
2/(b-a)
ответ: 2/(b-a)
3) (a+b/a^2-ab-1/a):b/b-a
a(b/a-b-1):b/b-a (a-сокращаем)
(b/a-b-1):b/b
1) b-ab-a=b-ab
a
2) b-ab:b/b=ab(умноженная) b
3)0.5(умножен)7-2(умножен)7-2= -12,5
ответ: -12,5
Объяснение:
Мы имеем дело с алгебраической дробью. Вспоминаем теорию:
чтобы сложить или вычесть алгебраические дроби, нам надо привести их к общему знаменателю.
Так как тут число, которое делится на знаменатели 6 + x и x - 7 нельзя подобрать, то мы просто умножим эти два знаменателя.
Получаем общий знаменатель - (6 + x) * (x - 7).
Далее мы ищем доп.множители.
Когда мы решаем примеры с обыкновенными дробями, то мы общий знаменатель делим на знаменатели дробей.
Но когда мы имеем дело с алгебраическими дробями, то в качестве доп.множителей у нас будут недостающие элементы:
У первой дроби доп.множитель x-7, а у второй - 6 + x.
Получаем дробь:
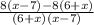
Далее мы раскрываем скобки:
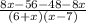
(Если забыл как раскрывать скобки: мы умножаем число перед скобкой на два числа в скобках. Например: 2(a + b) = 2 * a + 2 * b = 2a + 2b).
Ну а дальше мы сокращаем 8x и -8x (они с разными знаками). -56 - 48 даст нам -104.
Получим: -104/(6 + x) (x - 7).
Задача решена.
Понятно ли я объяснил материал?
Из них 3 благоприятствующих.
P=3/8=0,375