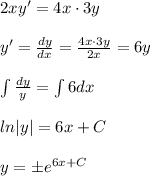
1) Т. к треуг. ABC - равнобедренный, BM является медианой и высотой.
Площать треуг. AOC= площадь. треуг. AOM + площадь. треуг. OMC
треугольники AOM и OMC равны по двум катетам (OM - общий катет, AM=MC, т.к. BM - медиана), значит и их площади равны. Значит, Площать треуг. AOC=2* площадь. треуг. OMC.
площадь. треуг. OMC. - это половина произведения катетов, т.е. (OM*MC)/2.
Т.к. BM - медиана, AM=MC=8:2=4 (см)
Т.к. точкой пересечения медианы делятся в отношении 2:1, то
BO/OM=2/1, т.к. BM=9, то BO=9-OM
Подставив это равенство в пропорцию, получаем:
(9-OM)/OM=2/1
Выразив из пропорции (9-OM) получаем:
9-OM=2OM
3OM=9
OM=3
Осталось подставить найденные величины в формулу площади треугольника.
площадь. треуг. OMC=(3*4)/2=6 (см)
Тогда площадь треугольника AOC= 2*6=12 (см)
ответ: площадь треугольника AOC=12 см
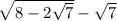
тут мы иммем дело с разницей квадрата под корнем. его надо уметь видеть.
= 
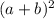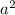+ 2ab +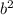 
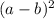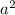= - 2ab +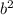
в данном случе второе(минус перед два корней из семи).
И так 2√7 - в данном случае это у нас 2ab.
8 - это сума а в квадрате и б в квадрате.
то есть:
8 = +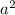
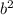
2ab = 2√7
ab = √7
То есть нам нужно методом подбора подобрать такие числа, чтобы их сумма в квадрате была 8, а при умножении они давали корень из семи. (тут метод подбора ничего более просто нужны тренировки и практика для этого).
Я подобрала:
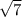и 1. И в правду, 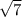* 1 =[/tex]\sqrt{7}[/tex]
и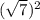 
+ 
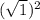= 7 + 1 = 8
то есть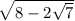 
= 
= |
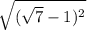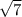- 1| (по модулю, модуль убираем, ибо 
|
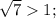То есть:
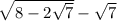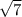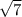= - 1 - = -1.
ответ: -1.
