если решаете уравнение без привязки к Вашим ответам,то решение:(-1) в степени к+1 и так далее...
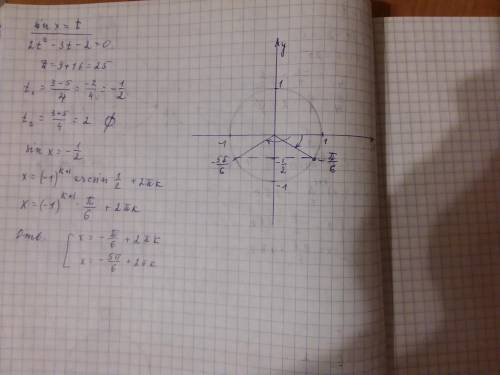
если же нужно выбрать ответ,тогда рисуете единичный круг.
Пусть собственная скорость лодки x [км/ч], тогда скорость лодки по течению x+2 [км/ч] и против течения x-2 [км/ч].
Время, затраченное на первый отрезок пути: 16/(x-2) [ч],
на второй отрезок пути: 12/(x+2) [ч].
Общее время в пути: 16/(x-2) + 12/(x+2) = 3 [ч]
x <>2 и x <> -2, домножаем обе части уравнения на (x+2)*(x-2), получаем:
16*(x+2) + 12*(x-2) = 3*(x+2)*(x-2)
16*x + 32 + 12*x - 24 = 3* x^2 - 12, где x^2 = x*x
28*x + 8 = 3* x^2 - 12
3*x^2 - 28*x - 20 = 0
Дискриминант: D = b^2 - 4*a*c = 28*28 - 4*3*(-20) = 1024 = 32^2
x1 = (-b + sqrt(D))/(2*a) = (28 + 32) / 6 = 10 [км/ч]
x2 = (-b - sqrt(D))/(2*a) = (28 - 32) / 6 = -2/3 [км/ч]
Второй корень логически не имеет смысла, поэтому ответ: 10 км/ч.
Это по сути квадратное уравнение. Замена sin x = t
2t^2 - 3t - 2 = 0
D = 9 - 4*2(-2) = 9 + 16 = 25 = 5^2
t1 = sin x = (3 + 5)/4 = 8/4 = 2
Решений нет.
t2 = sin x = (3 - 5)/4 = -2/4 = -1/2
x1 = -П/6 + 2П*k
x2 = П+П/6 + 2П*k = 7П/6 - 2П + 2П*k = -5П/6 + 2П*k
ответ: d.