(a+b-c)^2 = a*a + b*b + c*c + 2ab -2ac -2bc
2ab -2ac -2bc = (a+b-c)^2 - a*a + b*b + c*c = 49 - 21 = 28
ab -ac -bc = 28/2 = 14
1)Найдите девятый член последовательности
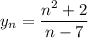

2) Найдите пятый член последовательности заданной рекуррентным у1 = ½, yₙ=2*y₍ₙ₋₁₎
y₂=2*1/2=1; y₃=2*1=2; y₄=2*2=4; y₅=2*4=8
3) Подберите формулу n- го члена последовательности - 2/2; 4/5; - 6/8; 8/11; -10/14;

проверка:
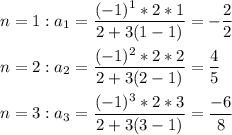
4) Сколько членов последовательности 3, 6, 9, 12,….меньше числа 95
аₙ=а₁+3(n-1)
aₙ<95
a₁+3(n-1)<95
3+3n-3<95
3n<95
n<31.(6)
n=31
проверим: a₃₁=3+3(31-1)=3+3*30=93
Значит 31 член меньше 95
5) у₁ = 2, у₂ = 1, уₙ = 2y₍ₙ₋₂₎+3y₍ₙ₋₁₎ (n = 3,4,5,…).Найдите n, если известно, что уₙ = 83.
тут можно просто решить находя слены этой последовательности
y₁=2
y₂=1
y₃=2*2+3*1=4+3=7
y₄=2*1+3*7=2+21=23
y₅=2*7+3*23=14+69=83
N=5
a² + b² + c² = 21
a + b - c = 7
(a + b - c)² = 7²
[(a + b) - c]² = 49
(a + b)² - 2 * (a + b) * c + c² = 49
a² + 2ab + b² - 2ac - 2bc + c² = 49
(a² + b² + c²) + 2ab - 2bc - 2ac = 49
21 + 2(ab - bc - ac) = 49
2(ab - bc - ac) = 28
ab - bc - ac = 14