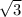Мачта укрепляется с растяжек, длина которых равна 10 м, а угол наклона их к горизонтальной плоскости равен 60 градусов. на какой высоте к мачте прикреплены растяжки ?
Иначе говоря, нужно придумать прямоугольник такой формы, чтобы его площадь была равна 400 кв.м, а периметр был наименьшим. ответ: это квадрат со стороной 20 м. Докажем это так. Нам нужно построить функцию периметр от сторон S = a*b; b = S/a P = 2(a+b) = 2(a + S/a) -> min Найдем точку минимума, приравняв производную к 0. P ' = 2(1 - S/a^2) = 0 S/a^2 = 1 a^2 = S a = √S; b = S/a = S/√S = √S = a Таким образом, a = b = √S = √400 = 20, то есть поле - это квадрат. Периметр равен P = 20*4 = 80 м. Площадь полосы деревьев равна 80*10 = 800 кв.м.
Получается прямоугольный треугольник. Угол между мачтой и растяжками равен 90-60 = 30 градусов. Следовательно, горизонтальный катет равен 10/2 = 5. Далее используем теорему Пифагора:
с^2 = a^2 + b^2
с известно, а тоже, выражаем нужную величину:
b =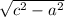
b =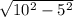 =
= 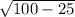 =
= 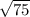 =
=
5