 k є Z
k є Z
Объяснение:Найти производную следующих функций:
1) у = 4х^4 + 3х; y'= (4x⁴+3x)'= 16x³+3
2) у = 12х^2 - х – 2; y'= (12x²-x-2)' =24x - 1
3) у = -4х^9 - 8х^4 – 6х + 22; y' = (-4x⁹-8x⁴-6x+22)= - 36x⁸-32x³-6
4) у= 8х^7 - 14х^5 + 5х - 10; y' =(8x⁷-14x⁵+5x-10)'= 56x⁶-70x⁴+5
5) у = 6х^3 + (1/9)х^3 + 9х; y'= 18x²+(1/3)x²+9
6) у = 19х^4 + 3х^8 – 22. y'=76x³+24x⁷
«Производная степенной, логарифмической и показательной функций»
Найти производную следующих функций:
1. у = (х - 2)^8 y' = 8(x-2)⁷(x-2)'=8(x-2)⁷
2. у = (х2 + 2х)^3 y'= 3(x²+2x)²(x²+2x)'= 3(x²+2x)(x+2)=3x(x+2)²= 3x(x²+4x+4)=3x³+12x²+12x
3. у = (х +3)^4 y'=4(x+3)³(x+3)'= 4(x+3)³ =4( x³+9x²+27x+27)
4. у = 41^х y' = 41ˣ ln41
5. у = (3 + 5х + х3)^2 y' = 2( x³+5x+3)( x³+5x+3)'= 2( x³+5x+3)(2x+5)
Задание 1. Решить уравнения.
а) 1,2(x - 3) + 0,4(1 - x) = 4
1,2x - 3,6 + 0,4 - 0,4x = 4
1,2x - 0,4x = 4 + 3,6 - 0,4
0,8x = 7,2
x = 7,2 : 0,8 = 9
ответ: 9
б) Здесь, очевидно, что в числителях забыли скобки:
(2 - 3x)/4 + (1 - x)/2 = (4 - 3x)/8
Умножим всё уравнение на 8
2(2 - 3x) + 4(1 - x) = 4 - 3x
4 - 6x + 4 - 4x = 4 - 3x
4 + 4 - 4 = 6x + 4x - 3x
7x = 4
x = 4/7
ответ: 4/7
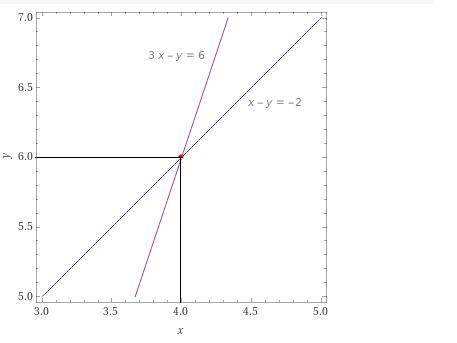
Задание 2. Определить количество решений системы графическим методом. Записать алгоритм построения графиков.
Здесь надо построить графики и найти, где они пересекаются.
{ x - y = -2
{ 3x - y = 6
Выразим игреки через иксы:
{ y = x + 2
{ y = 3x - 6
Они пересекутся в точке (4; 6).
ответ: Решение единственное и оно показано на рисунке.
Задание 3. Решить систему уравнений.
Здесь, очевидно, в числителях опять забыли скобки, как в 1. б):
{ (x + 4)/5 - (y - 1)/8 = 1
{ (x + 2)/9 - (y - 3)/6 = 2/3
Умножаем 1 уравнение на 40, а 2 уравнение на 18:
{ 8(x + 4) - 5(y - 1) = 40
{ 2(x + 2) - 3(y - 3) = 12
Раскрываем скобки:
{ 8x + 32 - 5y + 5 = 40
{ 2x + 4 - 3y + 9 = 12
Приводим подобные:
{ 8x - 5y = 40 - 32 - 5 = 3
{ 2x - 3y = 12 - 4 - 9 = -1
Умножаем 2 уравнение на -4:
{ 8x - 5y = 3
{ -8x + 12y = 4
И складываем уравнения:
8x - 5y - 8x + 12y = 3 + 4
7y = 7
y = 1
8x = 3 + 5y = 3 + 5*1 = 6
x = 1
ответ: (1; 1)
Задание 4. Составить математическую модель задачи и решить её.
Один сплав мед и цинка имеет массу m1 кг и содержит 8% цинка.
Второй сплав имеет массу m2 кг и содержит 24% цинка.
Вместе они дают сплав массой 300 кг, содержащий 12% цинка.
Найти массы начальных сплавов m1 и m2.
Во-первых, можно найти, что m2 = 300 - m1.
Во-вторых, сплавы содержат 0,08*m1 кг и 0,24(300-m1) кг цинка.
Конечный сплав содержит 300*0,12 = 36 кг цинка.
Математическая модель задачи - это уравнение:
0,08*m1 + 0,24(300 - m1) = 36
Решаем его. Раскрываем скобки:
0,08*m1 + 72 - 0,24*m1 = 36
72 - 36 = 0,24*m1 - 0,08*m1
0,16*m1 = 36
m1 = 36/0,16 = 3600/16 = 900/4 = 225 кг - масса 1 сплава.
m2 = 300 - m1 = 300 - 225 = 75 кг = масса 2 сплава.
ответ: 225 кг сплава 8% и 75 кг сплава 24%.