Сколько существует различных упорядоченных наборов (x,y,z) натуральных чисел x,y,z таких что x+y+z=14?
Таких упорядоченных наборов существует:
(14-1)! / ((3-1)! * (14-3)!) = 13! / (2! * 11!) = 12 * 13 / 2 = 6 * 13 = 78 наборов.
Сколько существует различных упорядоченных наборов (x,y,z) натуральных чисел x,y,z x+y+z=14 x>1,y>2,z>2 или z=2?
Я так понял, что нужно рассмотреть четыре отдельных случая с такими условиями "x>1,y>2,z>2 или z=2". Если нет, и нужно рассмотреть все эти 4 условия вместе, тогда я неправильно понял второй вопрос и нижний ответ вам не подходит.
При x > 1 таких упорядоченных наборов существует:
При y > 2 таких упорядоченных наборов существует:
При z > 2 (как и для y > 2) таких упорядоченных наборов существует:
При z = 2 таких упорядоченных наборов существует:
1)Чтобы найти координаты центра окружности, разделим диаметр на два радиуса, так как они равны, точка О делит диаметр в отношении один к одному, затем по формуле найдём координаты этой точки
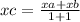
Где Хс - координата точки С по оси Х
Ха - координата точки А по оси Х
Хв аналогично
1 в знаменателе это их отношение, также 1 умножается на Хb.
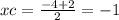
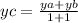
Аналогично и с этой формулой
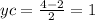
Тогда координатв центра (точки С) будет (-1;1)
2) Составим уравнение прямой, проходящей через точки А и С, уравнение прямой
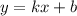
Для этого представим обе точки в уравнения и решим систему
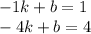
Умножим первое уравнение системы на - 4
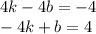
Из этого получаем уравнение
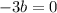
Отсюда
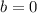
Если
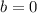
То поставив это значение в одно из уравнений системы найдём значение К
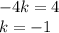
Следовательно уравнение примет вид
У=-х
3)Чтобы найти уравнение окружность, найдём радиус (его длинну) по координатам
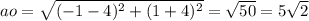
И поставим прежние вычисления в уравнение окружности
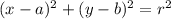
Где а и b координаты центра окружности ;
ao=r ;

1)Уравнение окружности
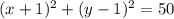
2)Уравнение прямой
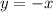
ищем через дискриминант
D=b^2-4ac
где б это 10 с противоположным знаком (в уравнении -10,значит берем 10),а-это первый коэффициент(в уравнении его не дано,где х^2 ,значит пишем единицу ),с-это самое последнее число берем с тем же знаком ,что и в уравнении.
Решаем
D= 10^2-4*1*25
D=100-100=0
х1=b+D:2a
x2=b-D:2a
подставляем b в числовом значении как было дано выше,потом корень и число получившееся в дискриминанте потом все это делим на 2 умноженное на числовое значение а.
x1=(10+корень из 0):2*1=10:2=5
х2=(10-корень из 0):2*1=10:2=5
ответ:х1=5,х2=5
тоже самое и с этим уравнением
2)4x^2-12x+9
Ищем дискриминант
D=b^2-4ac
D=12^2-4*4*9
D=144-144=0
x1=(12+корень из 0):2*4=12:8=1,5
х2=(12-корень из 0):2*4=12:8=1,5
ответ:х1=1,5,х2=1,5