По условию известно, что режимов освещения было не больше 5. То есть их могло быть:
1, 2, 3, 4, 5
Так как существует также полное отключение освещения, всего состояний может быть:
2, 3, 4, 5, 6
Найдем, сколько раз нужно нажать на кнопку, чтобы независимо от точного количества режимов вернуться в тот же самый режим. Для этого, нужно найти число, которое делится на 2, 3, 4, 5, 6 без остатка. То есть, другими словами нужно найти НОК этих чисел.
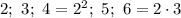
Таким образом, если нажать на кнопку 60 раз, то мы перейдем к такому же состоянию, с которого все начиналось.
По условию сейчас включен первый режим, также известно, что именно перед первым режимом идет состояние полного отключения. Значит, нажав на кнопку 60 раз мы вернемся к первом режиму, а если мы нажмем на кнопку на 1 раз меньше, то есть 59 раз, то мы полностью выключим свет.
Найденный является простейшим с той точки зрения, что нажать на кнопку можно и большее количество раз, а именно любое количество, задаваемое формулой 
, где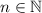 
, и свет также будет отключен.
ответ: нажать на кнопку 59 раз
1. Принимаем за х величину одного из чисел, за у значение другого числа.
2. Составим два уравнения:
(1) х + у = 18; х = 18 - у;
(2) ху = 65;
3. Подставляем значение х = 18 - у из первого уравнения во второе уравнение:
(18 - у)у = 65;
18у - у² = 65;
у² - 18у + 65 = 0;
Первое значение у = (18 + √324 + 4 х 65)/2 = (18 + √64)/2 = (18 + 8)/2 = 13.
Второе значение у = (18 - 8)/2 = 5.
Первое значение х = 18 - 13 = 5.
Второе значение х = 18 - 5 = 13.
ответ: значение одного из чисел 5, другого 13.
Объяснение:
1.5X-9=1.4X+7
0.1X=16
X=160
1) 0.7X-3.5=X-0.1
0.7X-X=3.5-0.1
-0.3X=3.4
X= -11.333(3)