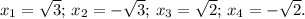1.Квадратным уравнением , называется уравнение вида ах² + bх + с =0, где x переменная a, b, c некоторые числа причем a не равно нулю 0
2. Числа а, b, с, называются коэффициентом квадратного уравнения.
3. Старший (первый) коэффициент
4. Второй коэффициент
5. Свободный член
6. Если в квадратном уравнении ах² + bх + с =0, хотя бы один из коэффициентов a или b, равен 0, то такое уравнение называется неполным квадратным уравнением.
7. Количество корней квадратного уравнения зависит от знака D
8.Дискриминант вычисляется по формуле Д=b^2 - 4ac
9.2 корня
10.не имеет корней
11. 1 корень
12.
х1=-b+√D/2a, х2=-b-√D/2a
Объяснение:
Я полагаю что в задании неточность. Функция должна по здравому смыслу такой:
у = 3х² + 6х + 2
типа у = ах² + вх + с,
где а = 3, в = 6, с = 2
График этой функции квадратна парабола веточками вверх, т.к а > 0.
вершина параболы имеет координаты
Хв = -в/2а = - 6/(2·3) = -1
Ув = 3 - 6 + 2 = -1
График функции пересекает ось х в точках, где у = 0
3х² + 6х + 2 = 0
D = 36 - 24 = 12
√D = √12 = 2√3 ≈ 3,464
х₁ = (-6 - 3,464):6 = -1,577
х₂ = (-6 + 3,464):6 = -0,423
для таблицы произведём подсчёты
х = 3 у = 3·9 + 6·3 + 2 = 47
х = 2 у = 3·4 + 6·2 + 2 = 26
х = 1 у = 3 + 6 + 2 = 11
х = 0 у = 2
х = -1 у = 3 + -6 + 2 = -1(минимальное значение)
относительно прямой х = -1 график симметричен, поэтому и значения функции в симметричных точках одинаковы
х = -2 у = 2
х = -3 у = 11
х = -4 у = 26
х = -5 у = 47
Составляем таблицу
х 3 2 1 0 -0,423 -1 -1,577 -2 -3 -4 -5
у 47 26 11 2 0 -1 0 2 11 26 47
ОДЗ: х≠±1
Замена: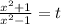 , t≠0
, t≠0
Возвращаемся к замене:
1)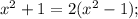
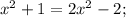
2)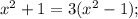
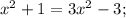
ответ: