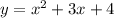
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
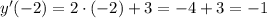
Уравнение касательной имеет вид:
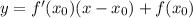
Подставим значение 
Итак, уравнение касательной заданной функции: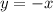 
Воспользуемся геометрическим смыслом касательной: коэффициент наклона 
касательной 
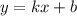численно равен тангенсу угла наклона 
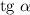с положительным направлением оси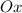 
В найденной касательной коэффициент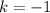 
, следовательно, 
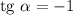при 
или 
ответ: или
9=3*3*1 две цифры одинаковые
8=4*2*1
7=7*1
6=3*2*1
5=5*1
4=4*1=2*2*1
3=3*1
2=2*1
легко увидеть, что из всех возможных комбинаций при данных ограничениях наибольшее целое число будет 8421