Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру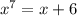 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
Уравнение имеет два различных корня при D > 0.
D = b^2 - 4ac = (2(a - 1))^2 - 4*(a^2 - 1)*2 = 4a^2 - 8a + 4 - 8a^2 + 8 =
= -4a^2 - 8a + 12 = -4(a^2 + 2a - 3)
D > 0 > -4(a^2 + 2a - 3) > 0
a^2 + 2a - 3 < 0
a^2 + 2a - 3 = 0
По теореме Виета а_1 = -3, а_2 = 1
Решением неравенства D > 0 , будет -3 < a < 1
ответ. (-3; 1)