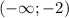Объяснение:
если известно, что искомая прямая y₁ = k₁x +b₁ параллельна прямой y=-4x+51 (у=кх +b), то мы знаем коэффициент k₁ = -4 при x, т.к. у параллельных прямых коэффициенты k и к₁ при х равны.
тогда мы уже имеем "половину" уравнения у₁ = -4х +b₁
теперь для определения b₁ используем то, что искомая прямая проходит через точку M(-1; 3). это означает, что координаты точки должны удовлетворять уравнению у₁ = -4х +b₁. подставим эти координаты
3= -4*(-1) +b₁ тогда b₁ = -1
и искомое уравнение
у₁ = -4х -1
теперь проверим, принадлежит ли построенному графику точка N(-50; 200). подставим ее координаты в уравнение у₁ = -4х -1
200 ≠ -4*(-50)-1
точка N(-50; 200) ∉ графику функции у₁ = -4х -1
тогда строим график по двум точкам
х = -1 у₁(-1) = 3 точка M(-1; 3)
х = 0 у₁(0) = -1
на первом фото построение по двум точкам у₁ = -4х -1 ║y=-4x+51
на втором показано, что точка N(-50; 200). ∉ графику у₁ = -4х -1

1° alogab=b - основное логарифмическое тождество.
2° logaa=1,a>0,a≠1
3° loga1=0,a>0,a≠1
4° loga(bc)=logab+logac - логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
5° logabc=logab−logac - логарифм частного.
Логарифм частного (дроби) равен разности логарифмов сомножителей.
6° logabp=p⋅logab - логарифм степени.
Логарифм степени равен произведению показателя степени на логарифм ее основания.
7° logakb=1k⋅logab
8° logab=1logba
9° logab=logcblogca - переход к новому основанию.
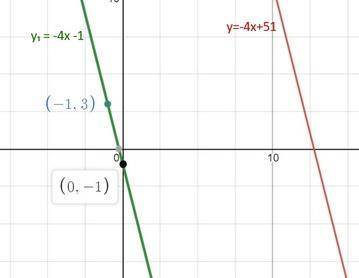
f(х)=3х+2
f(x)<-4
3x+2<-4;
3x<-4-2;
3x<-6;
x<-6/3;
x<-2
x є