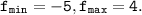Дана функция f(x)=2х-3∛(х^2 ) найти: а)критические точки функции f(x) на отрезке [-1; 8] б)наибольшее и наименьшее значение функции f(x) на отрезке [-1; 8]
В задаче отсутствует вопрос. Исхожу из предположения, что требуется определить время движения. t = S/v = 400/v. Но скорость задана не конкретным значением, а границами. Значит время можно только оценить. 50<v<80 заменим обратными числами,при этом меняем знак неравенства. 1/50 > 1/v > 1/80. Запишем в привычном виде: 1/80 < 1/v < 1/50. Теперь умножим все части неравенства на 400. 400/80< 400/v< 400/50. 5< t<8. Значит при заданных условиях время движения от 5 до 8 часов.
а) Критические точки:
б)![\tt \displaystyle f_{min},f_{max},x\in [-1;8]-?](/tpl/images/0338/5470/cc844.png)
f(-1) = 2·(-1)-3·![\sqrt[3]{(-1)^2}](/tpl/images/0338/5470/3c5e9.png) = -2-3 = -5
= -2-3 = -5
f(1) = 2·1-3·![\sqrt[3]{1^2}](/tpl/images/0338/5470/8986c.png) = 2-3 = -1
= 2-3 = -1
-5 < -1 ⇒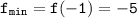
f(0) = 2·0-3·![\sqrt[3]{0^2}](/tpl/images/0338/5470/453f4.png) = 0-0 = 0
= 0-0 = 0
f(8) = 2·8-3·![\sqrt[3]{8^2}](/tpl/images/0338/5470/9dfdb.png) = 16-3·
= 16-3·![\sqrt[3]{2^6}](/tpl/images/0338/5470/a2068.png) = 16-12 = 4
= 16-12 = 4
4 > 0 ⇒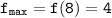
ответ: а) x = {0;1}; б)