(р-3)х^2-4рх+8р=0,
D=(-4p)^2-4(p-3)8p=16p^2-32p^2+96p=96p-16p^2,
D>0,
96p-16p^2>0,
96p-16p^2=0,
16p(6-p)=0,
p=0 или p=6,
-16p(p-6)>0,
p(p-6)<0,
0<p<6, p∈(0;6);
x1=(4p-4√(6p-p^2))/(2(p-3))>0,
x2=(4p+4√(6p-p^2))/(2(p-3))>0,
p-3≠0, p≠3;
(2p-2√(6p-p^2))(p-3)>0,
(2p+2√(6p-p^2))(p-3)>0,
2p-2√(6p-p^2)>0,
2p+2√(6p-p^2)>0,
p-3>0,
√(6p-p^2)<p,
√(6p-p^2)>-p,
p>3,
6p-p^2<p^2,
2p^2-6p>0,
2p^2-6p=0,
2p(p-3)=0,
p=0 или р=3,
p(p-3)>0,
p<0, p>3, p∈(-∞;0)U(3;+∞);
p∈(3,6);
2p-2√(6p-p^2)<0,
2p+2√(6p-p^2)<0,
p-3<0,
√(6p-p^2)>p,
√(6p-p^2)<-p,
p<3,
2p^2-6p<0,
p<0,
p<3,
0<p<3,
p<0,
p<3,
p∈Ф.
ответ: p∈(3,6).
Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через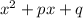
, другой - через 
.
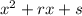Задача сводится к нахождению p, q, r, s. Тогда
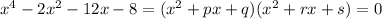
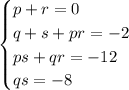
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
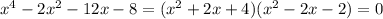
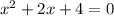не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).
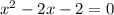
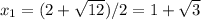
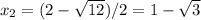
Сумма корней: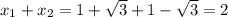 
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
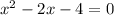
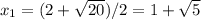
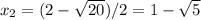
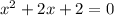не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).
Сумма корней: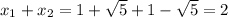 
ответ: 2.
= 3√7 - 1,5√7 - 3,5√7 + 4√7 = 2√7