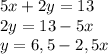
В решении.
Объяснение:
а) (х + 7)(х - 1) >= 0
В левой части неравенства квадратное уравнение, в котором
х₁ = -7, х₂ = 1.
График квадратичной функции - парабола.
Значения х - это точки пересечения параболой оси Ох, ветви вверх.
Представить эту параболу мысленно, или набросать схематично (ничего вычислять не нужно) и посмотреть, при каких значениях х парабола выше оси Ох (у >= 0, как в неравенстве).
Решение неравенства: х∈(-∞; -7]∪[1; +∞), объединение.
б) (х - 3)(х - 5) <= 0
Методика та же, что в предыдущем решении, только смотреть параболу ниже оси Ох:
х₁ = 3; х₂ = 5.
Решение неравенства: х∈[3; 5], пересечение.
в) (х - 2)(х + 3) < 0
х₁ = 2; х₂ = -3.
Решение неравенства: х∈(-3; 2), пересечение.
г) (а + 2)(а - 5) <= 0
а₁ = -2; а₂ = 5.
Решение неравенства: х∈[-2; 5], пересечение.
г) (t + 3)(t + 4) >= 0
t₁ = -3; t₂ = -4.
Решение неравенства: х∈(-∞; -4]∪[-3; +∞), объединение.
д) (2 - с)(3 - с) >= 0
-(c - 2) * -(c - 3) >= 0
(c - 2)(c - 3) >= 0
c₁ = 2; c₂ = 3
Решение неравенства: х∈(-∞; 2]∪[3; +∞), объединение.
Примечание: если знак >= или <=, неравенство нестрогое, скобка квадратная при числах. Знаки бесконечности всегда с круглой скобкой.
Если знак > или <, неравенство строгое, скобка круглая.
17(x + y) = 425
x + y = 25
y = 25 - x
Первый кран был открыт а часов, а второй кран а - 5 часов
ax + (a - 5)(25 - x) = 425
Если первый кран открыть на а - 5 часов, а второй на а часов, то через первый зальется в 2 раза меньше.
x(a - 5)*2 = (25 - x)*a
Получили систему из 2 уравнений с 2 неизвестными
{ ax + (a - 5)(25 - x) = 425
{ 2x(a - 5) = (25 - x)*a
Раскрываем скобки
{ ax + 25a - 125 - ax + 5x = 425
{ 2ax - 10x - 25a + ax = 0
Приводим подобные
{ 25a + 5x = 550
{ 3ax - 10x - 25a = 0
Делим 1 уравнение на 5 и выражаем х через а
{ 5a + x = 110, x = 110 - 5a
{ 3ax - 10x - 25a = 0
3a(110 - 5a) - 10(110 - 5a) - 25a = 0
Делим уравнение на 5 и раскрываем скобки
3a*22 - 3a^2 - 220 + 10a - 5a = 0
Меняем знак и приводим подобные
3a^2 - 71a + 220 = 0
D = 71^2 - 4*3*220 = 5041 - 2640 = 2401 = 49^2
a1 = (71 + 49)/6 = 120/6 = 20
a2 = (71 - 49)/6 = 22/6 < 5 - не может быть, потому что в уравнении было положительное число а - 5.
Значит, а = 20, а второй кран был открыт а - 5 = 20 - 5 = 15 часов.
Производительность кранов
x = 110 - 5a = 110 - 5*20 = 10 л/час, y = 25 - x = 25 - 10 = 15 л/ч