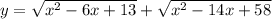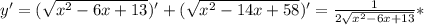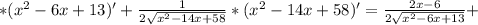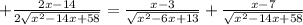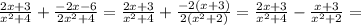
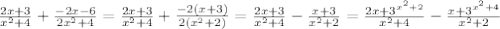
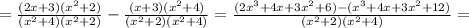
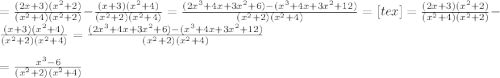 " alt="= \frac{(2x+3)( x^{2} +2)}{( x^{2} +4)( x^{2} +2)} - \frac{(x+3)( x^{2} +4)}{ ( x^{2} +2)( x^{2} +4)} = \frac{(2 x^{3} +4x+3 x^{2} +6)-( x^{3} +4x+3 x^{2} +12)}{ ( x^{2} +2)( x^{2} +4)} \\ \\ =\frac{ x^{3} -6}{( x^{2} +2)( x^{2} +4)}" />" />
" alt="= \frac{(2x+3)( x^{2} +2)}{( x^{2} +4)( x^{2} +2)} - \frac{(x+3)( x^{2} +4)}{ ( x^{2} +2)( x^{2} +4)} = \frac{(2 x^{3} +4x+3 x^{2} +6)-( x^{3} +4x+3 x^{2} +12)}{ ( x^{2} +2)( x^{2} +4)} \\ \\ =\frac{ x^{3} -6}{( x^{2} +2)( x^{2} +4)}" />" />