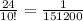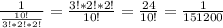1) (a + 8)^2;
(a+8)^2=a^2+16a+ 64
2) (b − 2)^2;
(b-2)^2=b^2-4b+4
3) (7 + c)^2;
(7+c)^2=49+4c+c^2
4) (6 − d)^2;
(6-d)^2=36-12d+d^2
5) (2m + 1)^2;
(2m+1)^2= 4m^2+4m+1
6) (4x − 3)^2;
(4x-3)^2=16x^2-24x+9
7) (5m − 4n)^2;
(5m-4n)^2=25m^2-40mn+16n^2
8) (10c + 7d)^2;
(10c+7d)^2=100c^2+140cd+49d^2
9) (4x − 1/8y)^2;
(4x-1/8y)^2=16x^2-y+1/64y^2
10) (0,3a + 0,9b)^2;
(0,3a+0,9b)=0,09a^2+0,27ab+0,81b^2
11) (c^2 − 6)^2;
(c^2-6)^2=c^4-12c^2+36
12) (15 + k^2)^2;
(15+k^2)^2=225+30k^2+k^4
13) (m^2 − 3n)^2;
(m^2-3n)^2=m^4-6m^2 n+9n^2
14) (m^4 − n^3)^2;
(m^4-n^3)=m^8-2m^4 n^3+ n^6
15) (5a^4 − 2a^7)^2.
(5a^4-2a^7)^2= 25a^8-20a^11+4a^14
Объяснение: