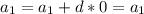проверено.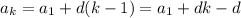
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
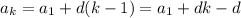то прибавив к данному выражению d. Мы получим следующий член .![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
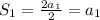. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
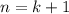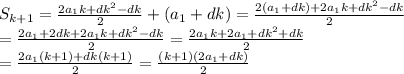
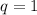получается деление на ноль, поэтому сразу пишем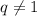 
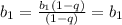
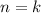
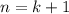:![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
а) х+19=30
х=30-19
х=11
11+19=30 (это проверка)
30=30
б) 27-х=27+х
х+х=27-27
2х=0
х=0:2
х=0
27-х=27+х
27-0=27+0
27=27
в) 30+х=32-х
х+х=32-30
2х=2
х=2:2
х=1
30+х=32-х
30+1=32-1
31=31
г) 10+х+2=15+х-3
(10+2)+х=(15-3)+х
12+х=12+х
х+х=12-12
2х=0
х=0:2
х=0
10+0+2=15+0-3
12=12
10+х+2=15+х-3
х=9
10+9+2=15+9-3
21=21
10+х+2=15+х-3
х=5
10+5+2=15+5-3
21=21
Если он к каждому привяжет по овце, то одна останется. Т.е. 3 + 1 = 4.
Если же он к каждому колышку привяжет по две овцы, то один колышек останется свободным. Т.е. 2*2=4, а 1 колышек остался.