1. Сумма углов n-угольника равна 180°(n-2).
В случае 12-угольника сумма равна 1800 градусов. Т. к. он правильный, то углы его равны 1800/12=150 градусов. ответ : 150°
2. Площадь параллелограмма равна произведению его основания (a) на высоту (h):
S = a ⋅ h
144 см² = а ⋅ 16 см
a = 9 см
3.s = a * b / 2
a - катет b - катет
a = 12
b^2 = 13^2 - 12^2
b^2 = 169 - 144
b^2 = 25
b = 5
S = 5 * 12 / 2
S = 30
4. Площадь ромба можно найти по формуле S = 0,5d₁d₂, где d₁ и d₂ - его диагонали.
Т.к. ромб - это параллелограмм, у которого все стороны равны, то он обладает всеми свойствами параллелограмма, а именно: диагонали ромба точкой пересечения делятся пополам. Значит, полусумма диагоналей равна 28 : 2 = 14 (см).
Свойство ромба: диагонали ромба перпендикулярны. Значит, при пересечении диагоналей ромба получаются 4 прямоугольных треугольника, у которых катеты - половины диагоналей, а гипотенуза - сторона ромба.
Рассмотрим один из прямоугольных треугольников и, применив теорему Пифагора, найдем его катеты.
Пусть один из катетов х см, тогда второй будет равен (14 - х) см. Т.к. сторона ромба равна 10 см, то составим и решим уравнение:
х² + (14 - х)² = 10²,
х² + 196 - 28х + х² - 100 = 0,
2х² - 28х + 96 = 0,
х² - 14х + 48 = 0.
D = (-14)² - 4 · 1 · 48 = 196 - 192 = 4; √4 = 2
х₁ = (14 + 2)/(2 · 1) = 16/2 = 8, х₂ = (14 - 2)/(2 · 1) = 12/2 = 6
Если один из катетов равен 8 см, то второй будет равен 14 - 8 = 6 (см). Тогда диагонали ромба будут равны 16 см и 12 см, а площадь
S = 0,5 · 16 · 12 = 96 (см²)
Если один из катетов равен 6 см, то второй будет равен 14 - 6 = 8 (см). Тогда диагонали ромба будут равны 12 см и 16 см, а площадь
S = 0,5 · 12 · 16 = 96 (см²)
ответ: 96 см².
5.Обозначим трапецию АВСД. угол С=угол Д=90 градусов. так как в трапецию можно вписать окружность, то суммы противоположных сторон равны ВС+АД=СД+АВ.
проведём высоту ВК. Она разделила трапецию на прямоугольник ДСВК и прямоугольный треугольник АВК. Так как острый уголА = 45 градусов, то второй острый угол АВК = 90-45=45 градусов, значит треугольник равнобедренный, ВК=АК.
Пусть АК=х тогда и ВК=х, по т. Пифагора х²+х²=(12√2)², 2х²=144·2, х²=144, х=12, АК=12 см, ВК=12 см, тогда и СД=12 см.S(ABCD)=1/2·(АД+ВС)·ВК=1/2·(12+12√2)·12=72·(1+√2)
17
Объяснение:
Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
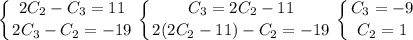
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит,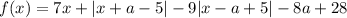 
. График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
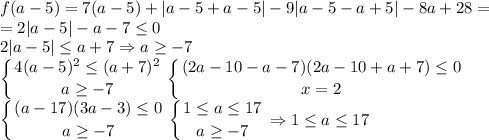
Наибольшее значение параметра — 17.
1л=0,001м³
5 000 000л=5000м³
5000/10000=5/10=1/2=0,5м- высота