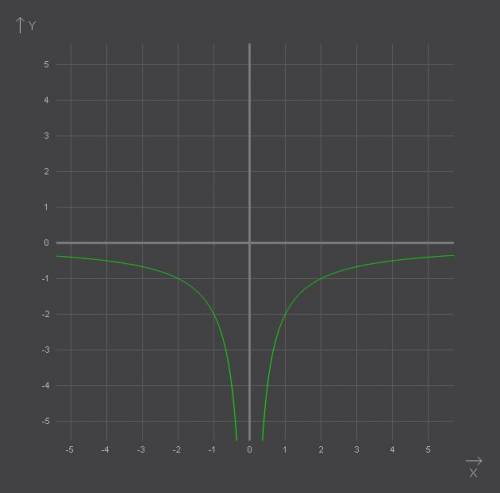
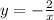 представляет собой стандартную гиперболу
представляет собой стандартную гиперболу 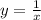 , растянутую в 2 раза от оси абсцисс и отображенную симметрично относительно оси абсцисс.
, растянутую в 2 раза от оси абсцисс и отображенную симметрично относительно оси абсцисс. 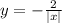 нужно часть графика
нужно часть графика 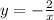 , расположенную в левой полуплоскости, стереть, и отобразить в эту полуплоскость симметрично оси ординат часть графика, расположенную в правой полуплоскости.
, расположенную в левой полуплоскости, стереть, и отобразить в эту полуплоскость симметрично оси ординат часть графика, расположенную в правой полуплоскости.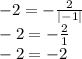

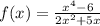
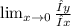
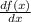
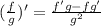
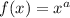
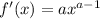
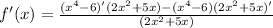
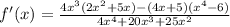
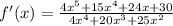
Решаем методом подстановки. Подставляем первое во второе.
x+x²-14=6
x²+x-20=0
D=1²-4(-20)=81
√D=9
x₁=(-1-9)/2=-5
x₂=(-1+9)/2=4
Подставляем найденное значение в первое уравнение
y₁=5²-14=11
y₂=4²-14=2
Таким образом, имеем две точки пересечения: (-5; 11) и (4; 2)
ответ: (-5; 1) и (4; 2)