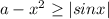
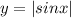расположен выше оси ОХ. 
.
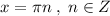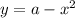- это параболы , ветви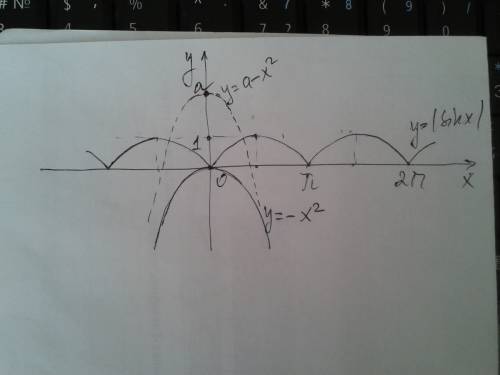
пусть пешеход, вышедший из А, после встречи км. Тогда его скорость v1=S/t =
= 3x/2 км/час (40 мин = 2/3 час).
Пешеходу, вышедшему из В, после встречи пришлось пройти x + 2 км. Тогда его скорость
v2=S/t = 2(x+2)/3 км/час (1 час 30 мин = 3/2 час).
До встречи первый затратил время t = (x+2)/v1 = 2 * (x+2)/(3x).
До встречи второй затратил время t = x/v2 = 3 * x/(2(x+2)). Времена затраченные до встречи равны. Составляем уравнение.
(2x + 4)/3x = 3x/(2x+4)
(2x + 4)² = 9x²
либо 2x + 4 = 3x. x=4, либо
2x + 4 = -3x. x=-4/5 (не имеет смысла).
Искомое расстояние S = x + x + 2 = 4 + 4 + 2 = 10 км
(х^2-6х+8)^3(х-8)^2 <или равно 0
первый множитель раскладываем на множители, предварительно найдя корни через Д или по т.Виета x1=4 x2=2
(x-2)^3(x-4)^3(х-8)^2 <или равно 0
на числовой луч наносим закрашенные точки 2; 4; 8
знаки+,-,+,+
ответ xe[2 ;4] в объединении {8}
знаки около 8 не меняются, т.к. скобка в четной степени
начинаем проверять знаки справа