ответ: 10
Объяснение:
(x+1)(x^2-x+1)-x(x+3)(x-3) Упростим данное выражение, для этого раскроем скобки. Также заметим, что (x+1)(x^2-x+1) - это формула сокращенного умножения: a³+b³=(a+b)(a²-ab+b²) , где, в нашем случае, a - это x, а b - это x, таким образом, (x+1)(x^2-x+1)=x³+1.
Заметим, (x+3)(x-3) - тоже формула сокращенного умножения - разность квадратов
(x+3)(x-3)=x²-9/ Преобразуем наше выражение, дораскрываем скобки:
(x+1)(x^2-x+1)-x(x+3)(x-3)=x³+1-x(x²-9)=x³+1-x³+9x=9x+1.
Найдем значение выражение при x=1:
9*1+1=10.
1)Докажите нер-во: 1. 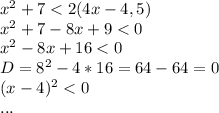
Не знаю, честно говоря что здесь требуется конкретно док-ть, прости. Т.к. тут квадрат меньше 0..
2.
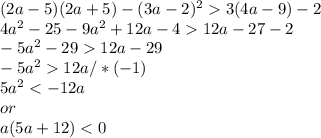
3.
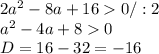
Вот тут могу док-ть и обосновать, т.к. данное квадратное ур-ие - вечный "плюс" и поэтому оно всегда будет больше 0 по определению. Вечный плюс, т.к. его дискриминант меньше 0.
2)Известно, что 7 <a <9. Оцените значение выражений:
1. a-3

2. -5a
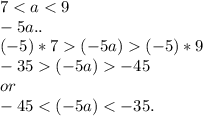
3) Дано 4 <a <3b, 2 <b <3 Оцените значение выражений: 1. а-3b
2. b-4а
3. ab
Не могу подсказать, забыла как это делать:с. Могу до утра еще исправить, если время будет. Условие я правильно записала твоих заданий?
2) b4 = b1·q3 5 = b1·q3
b6 = b1·q5⇒ 20 = b1·q5 Разделим второе уравнение на первое
q^2 = 4
а) q = 2 б) q = -2
5 = b1 ·2^3 5 = b1·(-2)^3
b1 = 5/8 b = -5/8
bn = b1·q^(n-1)
6561 = 9·3^(n-1)
3^(n-1) = 6561/9 = 729=3^5
n-1 = 5
n = 6