35 км/ч
Объяснение:
Дано:
S₁ = 35 км
S₂ = 34 км
t = 2 ч
Vр = 1 км/ч
V - ?
1)
Заметим, что собственная скорость лодки равна скорости ее движения по озеру:
V₁ = V
Время, затраченное на движение по озеру:
t₁ = S₁ / V₁
или
t₁ = S₁ / V.
2)
Время, затраченное на движение по реке.
Заметим, что река впадает в озеро, а это значит, что лодка двигалась против течения: V₂ = V - Vp
t₂ = S₂ / V₂ или
t₂ = S₂ / (V - Vp)
3)
Общее время движения:
t = t₁ + t₂
или
t = S₁ / V₁ + S₂ / (V - Vp)
Подставляем данные и решаем уравнение:
2 = 35 / V + 34 / (V - 1)
2·V·(V-1) = 35·(V-1) + 34·V
2·V² - 2·V = 35·V - 35 +34·V
2·V² - 71·V + 35 = 0
Решая это квадратное уравнение, получаем:
V = (71-69)/4 = 0,5 км/ч (слишком маленькая скорость...)
V = (71+69)/4 = 35 км/ч
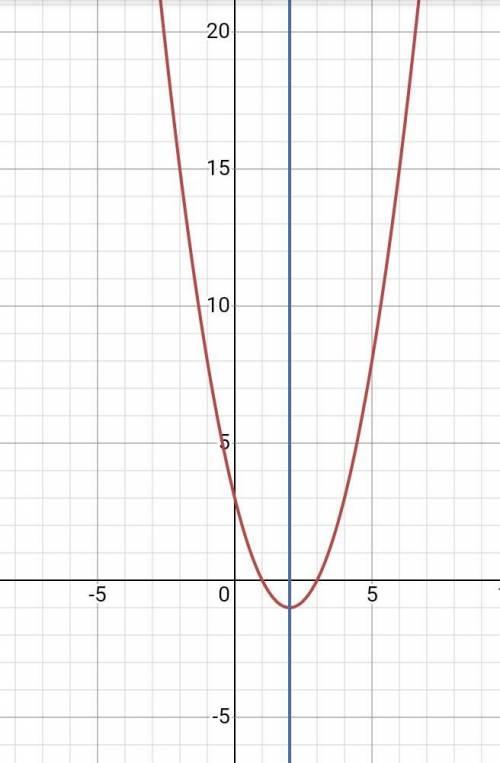
Объяснение:
а). D(y)=R
б). E(y)=R
в). Находим первую производную функции:
y' = 2·x-4
Приравниваем ее к нулю:
2·x-4 = 0
x1 = 2
Вычисляем значения функции
у(2) = -1
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y'' = 2
Вычисляем:
y''(2) = 2>0 - значит точка x = 2 точка минимума функции.
г). Ось симметрии параболы проходит через вершину и перпендикулярно оси Х. Координата х вершины:
х = -b/(2a) = (-4)/2 = -2
Уравнение оси симметрии: х=2 (смотри график)
д). х²-4х+3=0
х1=1, х2=3
=9²-a²=(9-a)(9+a)
=5(x-y)(x+y)
3(x²-2xy+y²)=3(x-y)²