Пусть числитель дроби равен x, тогда её знаменатель равен x+1. Если увеличить числитель на 5, то мы получим новый числитель x+5, а новы знаменатель будет следующим x+1-5=x-4. Т.к. получившаяся дробь равна 4, то составим уравнение:
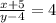
4*(x-4)=x+5
4x-16=x+5
3x=21
x=7
Т.е. это дробь 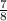
1. 1) положителен
2. 3) невозможно определить знак.
Объяснение:
приведенное квадратное уравнение имеет вид
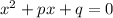
коэфициент при 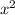 : a=1;
: a=1;
по теореме Виета :
свободный член
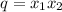
второй коэфициент
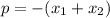
поэтому в случае 1 ответ 1) положителен, так как произведение двух чисел одинакового знака дает положительное число (плюс на плюс дает плюс и минус на минус дает плюс)
в случае 2 ответ 3) неозможно определить знак, так как к примеру при корнях -5 и 7 получим что второй коэффициент равен -2, а при корнях -7 и 5 получим что второй коэффициент равен 2

Исходная дробь имеет вид Х / (X +1). После прибавления к числителю 5 и вычитания от знаменателя 5 она приобретает вид (Х + 5) / (X - 4).
Поскольку значение этой дроби равно 4, получаем уравнение
Х + 5 = 4 * (Х - 4)
Х + 5 = 4 * Х - 16
3 * Х = 21
Х = 7
Итак, исходная дробь 7/8.