Скорость теплохода в стоячей воде равна 32,5 км/ч.
Объяснение:
Дано:
S₁ = 4 км против течения
S₂ = 33 км по течению
v = 6,5 км/ч -- скорость течения
T = 1 ч -- общее время
Найти: V -- скорость теплохода в стоячей воде
(V – v) -- скорость теплохода при движении против течения, поэтому на путь против течения теплоход затратил S₁ / (V – v) времени.
(V + v) -- скорость теплохода при движении по течению, поэтому на путь по течению теплоход затратил S₂ / (V + v) времени.
Общее время T равно сумме времени, которое теплоход шел по течению и против течения:
T = S₁ / (V – v) + S₂ / (V + v)
T(V – v)(V + v) = S₁(V + v) + S₂(V – v)
TV² – Tv² = (S₁ + S₂)V + (S₁ – S₂)v
TV² – (S₁ + S₂)V – Tv² – (S₁ – S₂)v = 0
Подставим числовые значения:
V² – (4 + 33)V – 6,5² – (4 – 33)·6,5 = 0
V² – 37V + 146,25 = 0
D = 37² – 4·146,25 = 784 = 28²
V₁ = (37 – 28)/2 = 9/2 = 4,5 км/ч -- не подходит, т.к. при такой скорости теплоход не смог бы двигаться против течения реки
V₂ = (37 + 28)/2 = 32,5 км/ч
5,6,7,8
Факт 1 и Факт 2 - неверные.
Кратко:
Попробуем сопоставлять по два факты, которые имеют смысл. Путем не сложных вичислений понимаем, что возможные числа находятся где-то между:
a ∈ (4, 8,25).
Обяснение:
Обозначим неизвесное число как a
Сопоставим 1 и 2:

a ∈ ∅
Сопоставим 2 и 4:
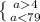
a ∈ (4, 79).
Сопоставим 2 и 3:
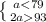
a ∈ ∅.
Получаем, что факт 1 и факт 3 не верные. Поскольку они не верные, мы можем смело их отразить (изменить > на <).
Теперь составим систему из 4 уравнений.
/ 2a < 93
| a > 4
| a < 79
\ 4a < 33
Решаем систему и получаем, что:
a ∈ (4, 8,25).
Отсюда берем целые числа. Тоесть получаем на ответ.
5,6,7,8
7cos²x=6
cos²x=6/7
cosx=√6/7 cosx=-√6/7
x=-+arccos√6/7+2πn x= -+arccos(-√6/7)+2πn n∈Z
2)sin²x-2cos²x+1/2sin2x=0
sin²x+sinx*cosx-2cos²x=0 поделим на cos²x≠0
tg²x+tgx-2=0
tgx=1 tgx=-2
x=π/4+πn x=-arctg2+πn
3) (sin²x+cos²x)(sin²x-cos²x)=sin²x
-cos²x=0
cosx=0
x=π/2+πn
4)sin²x+cos²x-3cos²x-2sinx*cosx=0
sin²x-2sinx*cosx-2cos²x=0 поделим на cos²x≠0
tg²x-2tgx-2=0
D=1+2=3
tgx=1+√3 tgx=1-√3
x=arctg(1+√3)+πn x=arctg(1-√3)+πn