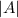- мощность множества A.
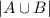- мощность объединения множеств A и B.
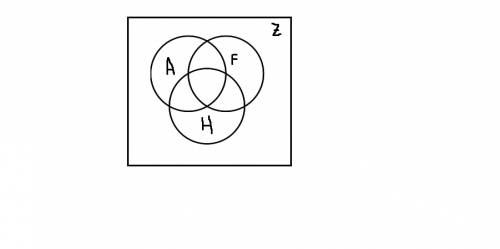
- мощность пересечения множеств A и B.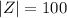
- кол-во всех студентов(обычно обозначают U - универсум, но я буду обозначать Z чтобы не путать его с знаком объединения U)
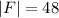- кол-во всех студентов изучающих французский.
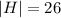- кол-во всех студентов изучающих немецкий.
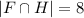- кол-во всех студентов изучающий и французский и немецкий.
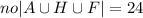(вместо no сверху черта отрицания над всем, не знаю как поставить) - студенты не изучающих иностранный язык.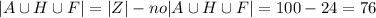
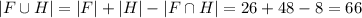
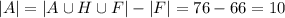
Дано линейное уравнение:
y = x2-8*x+1*y-x2+6*x+5
Приводим подобные слагаемые в правой части ур-ния:
y = 5 + y - 2*x
Переносим слагаемые с неизвестным x
из правой части в левую:
0 = 5 - 2*x
Разделим обе части ур-ния на 0
x = 5 - 2*x / (0)
Получим ответ: x = 5/2